Souper-Model How Simple Arithmetic Unlocks State-of-the-Art LLM Performance

🏷️ 논문 LLM Headliner

여러 개의 언어 모델을 평균화하는 방식만으로 새로운 모델을 훈련시키지 않고도 성능을 높일 수 있습니다. 단순 평균이 아니라 각 모델의 강점이 나타나는 부분을 찾아 비율을 다르게 섞는 SoCE를 제안합니다. 함수 호출 벤치마크에서 새로운 최고 성능을 달성했습니다.

논문 정보

제목: Souper-Model: How Simple Arithmetic Unlocks State-of-the-Art LLM Performance

저자: Shalini Maiti, Amar Budhiraja, Bhavul Gauri, Gaurav Chaurasia, Anton Protopopov, Alexis Audran-Reiss, Michael Slater, Despoina Magka, Tatiana Shavrina, Roberta Raileanu, Yoram Bachrach

소속: Meta SuperIntelligence Labs, FAIR at Meta, University College London

발행: 2025년 11월 (arXiv preprint)

S. Maiti, A. Budhiraja, B. Gauri, G. Chaurasia, A. Protopopov, A. Audran-Reiss, M. Slater, D. Magka, T. Shavrina, R. Raileanu, and Y. Bachrach, "Souper-Model: How Simple Arithmetic Unlocks State-of-the-Art LLM Performance," arXiv preprint arXiv:2511.13254, Nov. 2025. [Online]. Available: http://arxiv.org/abs/2511.13254.

대규모 언어 모델 개발은 자원과 시간을 요구합니다. 훈련 데이터 비율을 조정하거나 하이퍼파라미터를 변경하며 원하는 성능을 찾습니다. 이는 엄청난 연산량을 필요로 합니다. 이 문제를 해결하기 위해 이미 훈련된 여러 모델을 결합해서 성능을 높이는 Souping 방식을 개선합니다.

기존 연구들은 여러 모델의 가중치를 단순히 평균내는 방식(uniform souping)을 제시했습니다. 메타 연구진은 여기서 벤치마크의 카테고리별 성능 상관관계를 분석하여, 서로 다른 카테고리에서 각 모델이 다른 강점을 보인다는 것을 발견합니다. 이를 토대로 SoCE(Soup Of Category Experts)라는 방법을 제안했으며, Berkeley Function Calling Leaderboard에서 새로운 최고 성능을 달성했습니다.

이 접근법으로 이미 공개된 수십만 개의 오픈소스 모델들을 더 효과적으로 활용할 수 있을지도 모릅니다.

요약

항목	내용
핵심 기법	모델 Souping (weight averaging)과 카테고리 기반 최적화
주요 개선사항	균등 가중치 → 비균등 가중치 기반 결합
평가 벤치마크	Berkeley Function Calling Leaderboard (BFCL), MGSM, ∞-Bench, FLORES-101
아키텍처	Llama 3 기반 모델들 (8B, 70B 파라미터)
성능 향상	BFCL 70B: 78.56% → 80.68% (+2.7%), BFCL 8B: 72.37% → 76.50% (+5.7%)
핵심 통찰	벤치마크 카테고리 간 성능 상관관계가 낮을 때 expert 모델 식별 가능

상세 분석

1. 배경

현재의 대규모 언어 모델 개발 방식은 매우 반복적입니다. 기본 모델에서 시작하여 파인튜닝을 거치고, 다시 인간 피드백 강화학습을 적용합니다. 각 단계에서 훈련 데이터 구성을 조정하거나 하이퍼파라미터를 변경하는데, 이는 매우 높은 비용을 초래합니다. 논문 저자들이 주목한 점은 "이미 훈련된 모델들이 있다면, 이들의 강점을 결합할 수 없을까"라는 질문입니다.

모델 Souping의 기본 개념은 1990년대로 거슬러 올라가지만, 최근에 와서야 대규모 언어 모델에 체계적으로 적용되고 있습니다. 기존 방식(Wortsman et al., 2022)은 여러 모델의 가중치를 동일한 비율로 평균내는 방식이었습니다. 이 방식도 효과가 있었지만, 세밀한 최적화의 여지가 남아있었습니다.

메타의 Roberta Raileanu를 포함한 연구진은 한 가지 흥미로운 현상을 발견했습니다. 여러 모델들을 평가할 때, 특정 카테고리에서는 모델 간 성능이 높은 상관관계를 보이지만, 다른 카테고리에서는 거의 상관관계가 없다는 것입니다.

2. 카테고리 간 상관관계 분석

논문의 가장 중요한 발견은 Figure 1의 상관계수 히트맵에 담겨있습니다. Berkeley Function Calling Leaderboard 데이터를 분석하면, 모델 성능의 상관관계가 매우 이질적임을 알 수 있습니다.

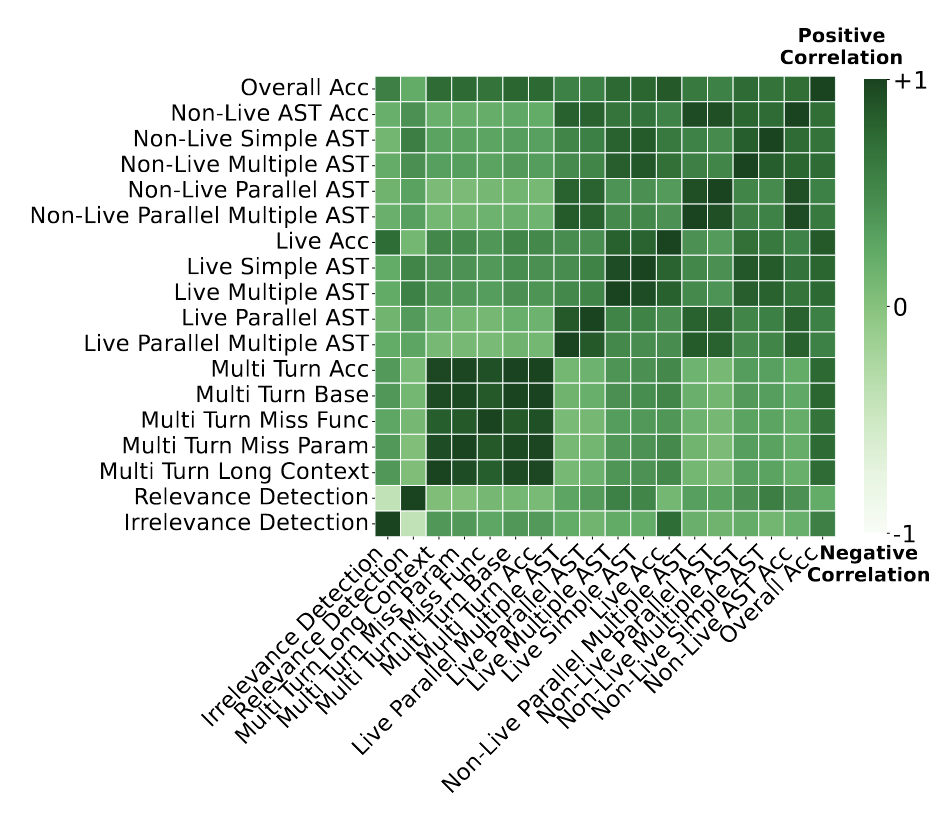
예를 들어:

높은 상관관계 (0.96-0.98): Multi-turn 관련 카테고리들 (Multi-turn base, Multi-turn miss parameter 등). 한 multi-turn 작업을 잘하는 모델은 다른 multi-turn 작업도 잘합니다.
낮은 상관관계 (0.07): Multi-turn-base와 Live Accuracy 카테고리. 이는 완전히 다른 역량 영역을 측정한다는 뜻입니다.

상관관계가 낮은 카테고리들은 각각 다른 "전문 모델"을 요구한다는 의미입니다. 높은 상관관계를 보이는 모델들을 모두 포함하는 것보다, 각 카테고리별로 가장 좋은 성능을 내는 모델을 선정하는 것이 더 효율적입니다.

3. SoCE

논문에서 제시하는 SoCE 방법은 네 가지 단계로 이루어집니다:

Step 1: 상관관계 분석 각 카테고리 쌍 사이의 Pearson 상관계수를 계산합니다. 임계값(τ)보다 낮은 상관관계를 보이는 카테고리들을 식별합니다. 이 카테고리들이 바로 "약한 상관관계" 카테고리 집합 L이 됩니다.

Step 2: Expert 모델 선택 각 약한 상관관계 카테고리에 대해, 그 카테고리에서 가장 높은 성능을 내는 모델을 "expert" 모델로 선정합니다. 예를 들어 Multi-turn-base에서 가장 좋은 모델 M*, Live Accuracy에서 가장 좋은 모델 M**를 선택합니다.

Step 3: 가중치 최적화 선택된 expert 모델들을 어떤 비율로 섞을지 결정합니다. 논문에서는 각 가중치를 0.1에서 0.9 사이에서 0.1 단위로 탐색했습니다. 모든 가중치의 합은 1이 되어야 합니다. 이 과정에서 벤치마크 전체 성능을 최대화하는 가중치 조합을 찾습니다.

\[w^* = \arg\max_w \sum_{i=1}^{l} \text{Performance}\left(\sum_{j=1}^{l} w_j \cdot M_j^*, C_i\right)\]

Step 4: 모델 Souping 최적 가중치 \(w^*\)를 사용하여 최종 모델을 생성합니다:

\[M_{\text{soup}} = \sum_{j=1}^{l} w_j^* \cdot M_j^*\]

가중치 최적화 과정은 계산 비용이 거의 없습니다. 이미 훈련된 모델들의 가중치를 선형결합하기만 하면 되기 때문입니다.

4. 실험 결과

Berkeley Function Calling Leaderboard (70B 모델)

개별 모델들의 성능:

xLAM-2-70b: 78.56%
CoALM-70B: 54.49%
watt-tool-70B: 73.57%
functionary-medium-70B: 62.32%

비교 결과:

Uniform Souping (모든 모델): 68.33%
Uniform Souping + SoCE 선택: 78.40%
SoCE (최적화된 가중치): 80.68% ← 새로운 최고 성능

무작정 모든 모델을 평균내면 오히려 성능이 하락했습니다(68.33%). 약한 모델이 강한 모델의 능력을 희석시키기 때문입니다. SoCE의 모델 선택 단계만 적용해도 78.40%로 향상되며, 여기에 가중치 최적화를 추가하면 80.68%에 도달합니다. 절대적 향상폭은 2.7%이지만, 상대적으로는 최고 성능 모델 대비 3.5% 향상입니다.

8B 모델 성능

더 작은 모델 그룹에서:

최고 성능 개별 모델: 72.37%
SoCE: 76.50% (+5.7% 상대 향상)

작은 모델 그룹에서 더 큰 향상이 있습니다. 선택 가능한 모델이 제한적일 때, 최적 조합의 가치가 더 크다는 의미입니다.

다른 벤치마크에서의 성능

BFCL뿐 아니라 다른 벤치마크에서도 검증했습니다:

MGSM (수학 능력): 50.9% → 51.7%
∞-Bench (긴 맥락): 27.44% → 28.0%

향상폭은 작지만, 최고 성능 개별 모델보다 여전히 우수합니다.

5. 모델 일관성

논문은 SoCE가 모델 일관성 향상에 기여한다고 주장합니다. Souping 이후 모델들의 카테고리별 성능이 더 높은 상관관계를 보인다는 것입니다.

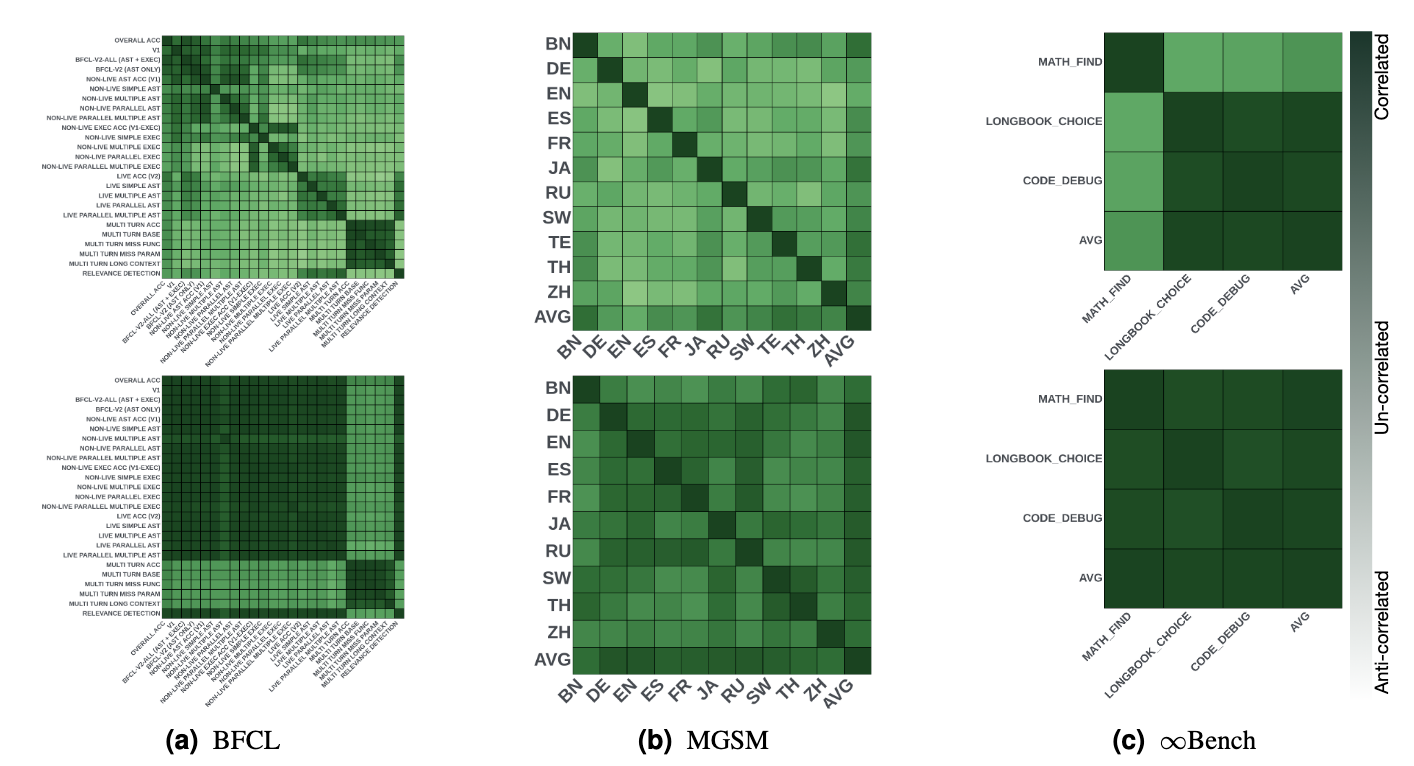
Figure 2를 보면 명확합니다. Souping 전에는 히트맵에 검정색(음의 상관관계)과 밝은 색(양의 상관관계)이 섞여있습니다. 하지만 Souping 이후에는 대부분 짙은 초록색(높은 양의 상관관계)으로 변합니다. 이는 Souped 모델이 모든 카테고리에서 더 균형잡힌 성능을 내놓는다는 의미입니다.

SoCE는 평균 성능 향상에 더해 모델이 다양한 작업에서 일관된 성능을 내도록 만듭니다. 이는 실무 환경에서 매우 중요한 특성입니다.

6. 협력 게임 이론을 통한 검증

논문은 Shapley value 분석을 추가로 제시합니다. 협력 게임 이론에서 Shapley value는 여러 플레이어가 협력했을 때 각 플레이어의 기여도를 공정하게 평가하는 지표입니다.

\[\phi_i = \frac{1}{n!} \sum_{\pi \in \Pi} [v(\text{pred}(a_i, \pi) \cup {a_i}) - v(\text{pred}(a_i, \pi))]\]

모델들을 '플레이어'로 보고, 각 모델 조합의 성능을 '협력의 결과'로 생각할 수 있습니다. Figure 3의 분석은 흥미로운 패턴을 보여줍니다:

약한 상관관계를 보이는 카테고리에서 전문성을 가진 모델들(M1, M2)이 높은 Shapley value를 보입니다.
약한 모델(M4)을 높은 가중치로 포함시키면 평균 성능이 크게 하락합니다 (47.0% → 37.0%).
SoCE가 선택한 모델 조합이 이론적으로도 최적의 기여도를 가짐을 시사합니다.

이는 SoCE의 선택이 단순한 경험적 최적화가 아니라 이론적 근거가 있음을 입증합니다.

7. 한계와 현실적 고찰

벤치마크 구조의 의존성

SoCE는 벤치마크가 의미있는 카테고리 분류를 이미 가지고 있을 것을 가정합니다. BFCL이나 MGSM처럼 명확한 카테고리 구분이 없는 벤치마크에서는 성능 향상이 미미합니다 (FLORES-36에서 실제로 향상폭이 작음).

같은 사전훈련 기반의 필요성

실험 대상은 모두 Llama 3에서 파생된 모델들입니다. 서로 다른 기반 모델을 Souping할 수 있는지는 아직 불명확합니다. 논문에서도 "같은 사전훈련 체크포인트가 필요한지 불명확"하다고 명시합니다.

훈련 단계 혼합의 위험

사전훈련 체크포인트와 파인튜닝된 모델을 섞으면 안 됩니다. 또한 정렬되지 않은 모델과 정렬된 모델을 섞으면 안전 문제가 발생할 수 있습니다.

Scaling 한계

모델을 계속 더 추가했을 때 성능이 계속 향상되는지, 아니면 어느 시점에서 수렴하는지는 체계적으로 검증되지 않았습니다.

결론

문제 인식: 기존 uniform souping은 모든 모델을 동일하게 취급하여 약한 모델이 강한 모델의 성능을 희석시킵니다.

해결책: 카테고리 간 성능 상관관계를 분석하여 각 약한 상관관계 집합에 대한 expert 모델을 식별하고, 비균등 가중치로 결합합니다.

성과와 한계: BFCL과 같은 잘 구조화된 벤치마크에서는 의미있는 성능 향상(+2-5%)을 보입니다. 다만 이는 이미 훈련된 모델들의 최적 활용일 뿐, 기본적인 모델 성능 향상에는 한계가 있습니다. 또한 벤치마크의 카테고리 구조에 크게 의존하며, 같은 기반 모델에서만 효과적입니다.

실무적 의의: 오픈소스 모델 생태계에서 SoCE의 가치는 분명합니다. 약 150,000개에 달하는 Llama 파생 모델들 중에서 의도한 용도에 맞는 모델들을 선택해 조합하면, 상당한 성능 향상을 거의 무료에 가깝게 얻을 수 있다는 점이 중요합니다. 이는 제한된 자원으로 활용 가능한 모델 개발이 필요한 연구자들이나 기업들에게 실질적인 도움이 될 것 같습니다.