LeJEPA Provable and Scalable Self-Supervised Learning Without the Heuristics

🏷️ 논문 LLM Headliner
1-LeJEPA.png

주요 성과:

R. Balestriero and Y. LeCun, "LeJEPA: Provable and scalable self-supervised learning without the heuristics," arXiv preprint arXiv:2511.08544, 2025.

JEPA(Joint-Embedding Predictive Architecture)는 자기 지도 학습의 유망한 방법론입니다. 기본 아이디어는 간단합니다. 같은 데이터의 서로 다른 관점(view)을 인코더에 통과시킨 후, 한 관점의 임베딩이 다른 관점의 임베딩을 예측하도록 학습시키는 것입니다.

그런데 문제가 있습니다. 이 예측 손실(prediction loss)만으로 학습하면 모든 입력을 동일한 임베딩으로 맵핑하는 표현 붕괴(collapse)가 발생합니다. 이를 막기 위해 업계는 여러 임시방편을 조합했습니다. Stop-gradient, teacher-student 네트워크, 명시적 정규화, 정교한 하이퍼파라미터 조정 등입니다.

LeJEPA는 이론으로 접근합니다. 다운스트림 작업의 위험(risk)을 최소화하려면 임베딩이 어떤 분포를 따라야 할까?

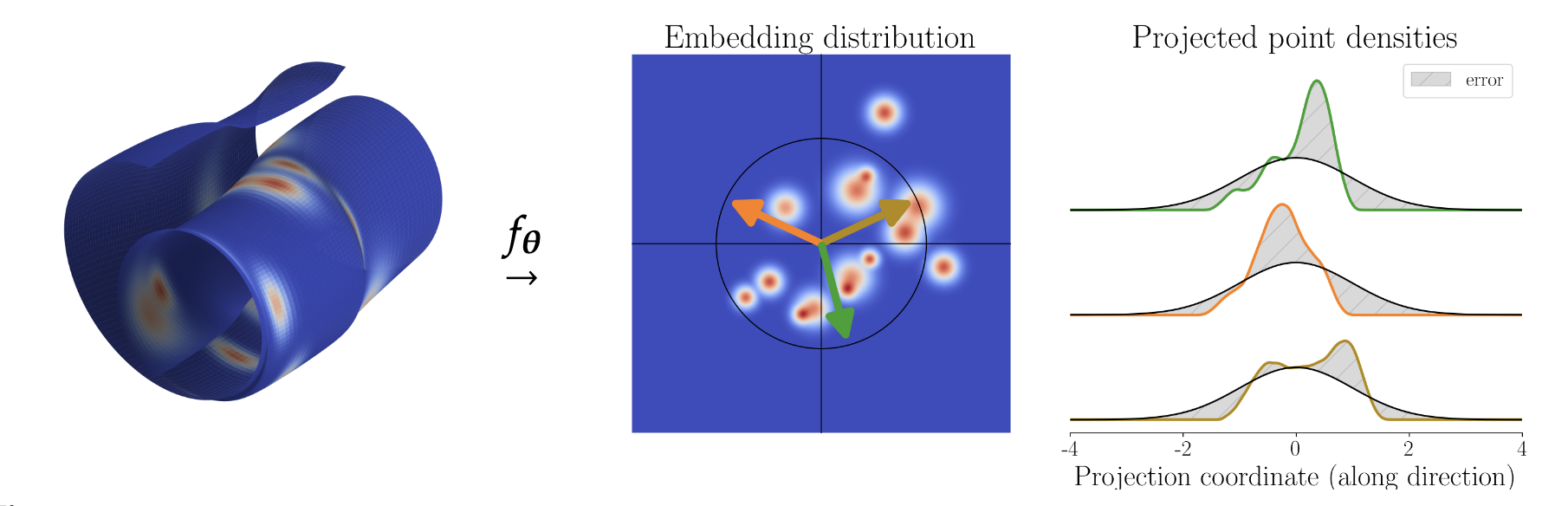
그 답은 놀랍게도 등방성 가우시안 분포(isotropic Gaussian distribution)입니다. 이를 증명한 후, 이 분포를 강제하는 정규화 항 SIGReg를 제시합니다. 결과적으로 모든 휴리스틱을 제거하고도 안정적으로 학습하는 LeJEPA를 만들 수 있습니다.

요약: 주요 메타데이터

기본 아키텍처: JEPA (Joint-Embedding Predictive Architecture)

핵심 혁신: SIGReg (Sketched Isotropic Gaussian Regularization) - 특성함수 기반 분포 매칭

메인 손실 함수: \[\mathcal{L} = (1-\lambda) \cdot \mathcal{L}_{\text{pred}} + \lambda \cdot \mathcal{L}_{\text{SIGReg}}\]

구성 요소:

복잡도: 시간/메모리 O(N) - 선형 (N은 배치 크기)

지원 모델: ResNet, ViT, ConvNeXt, MaxViT, Swin Transformers, EfficientNet 등 60개 이상

평가 데이터셋: ImageNet-1K/100, Galaxy10, Flowers102, Food101, CIFAR 등 10개 이상

평가 지표: 선형 프로빙(고정 인코더), k-NN 프로빙, 커널 방법

최고 성능:

논문 상세 분석

1. 문제 정의와 배경

자기 지도 학습은 라벨 없는 거대한 데이터로부터 의미 있는 표현을 학습하는 분야입니다. 오랫동안 두 가지 주요 패러다임이 지배했습니다:

  1. 슈퍼바이저 학습: 레이블로 직접 학습
  2. 재구성 기반: 원본 입력을 복원하도록 학습

최근 **JEPA(Joint-Embedding Predictive Architecture)**라는 새로운 패러다임이 등장했습니다.

그런데 근본적인 문제가 발생했습니다:

JEPA의 정의는 두 조건으로 요약됩니다:

  1. \(\text{Enc}(\mathbf{x}_{n,t+1})\)이 \(\text{Enc}(\mathbf{x}_{n,t})\)로부터 예측 가능해야 함
  2. 인코더의 임베딩이 퇴화(degenerate)하지 않아야 함

두 번째 조건이 모호했습니다. 실제로는 첫 번째 조건만으로는 표현 붕괴가 발생합니다. 왜냐하면 모든 입력을 상수 값으로 매핑하면 예측 손실이 0이 되기 때문입니다.

기존의 임시방편 해결책들:

방법

원리

한계

Stop-gradient

한쪽 분기의 기울기 차단

왜 작동하는지 불명확, 비대칭적

Teacher-student

천천히 업데이트되는 네트워크 복사본

EMA 스케줄 선택이 복잡, 메모리 증가

명시적 정규화

Whitening, 배치 정규화 추가

별도 모듈 필요, 구현 복잡

하이퍼파라미터 조정

각 설정마다 섬세한 튜닝

확장 불가능, 재현성 낮음

이 모든 것이 정말 필요할까? 수학적으로 더 깔끔한 해결책이 있지 않을까?

2. 핵심 이론: 등방성 가우시안

2.1 기본 질문 재설정

저자들이 던진 질문: 다운스트림 작업의 위험을 최소화하려면, 인코더의 임베딩 \(f_\theta(\mathbf{x})\)가 어떤 분포를 따라야 할까?**

이 질문의 아름다움은 구체적인 작업에 의존하지 않는다는 점입니다. 즉, 모든 가능한 다운스트림 작업에 대해 평균적으로 최선인 분포를 찾는 것입니다. 이를 두 가지 현실적인 평가 방식으로 분석합니다.

2.2 선형 프로빙 (Linear Probing)

가장 간단한 평가: 동결된 임베딩에 선형 회귀를 적용합니다.

임베딩 행렬 \(\mathbf{Z} \in \mathbb{R}^{N \times K}\) (N개 샘플, K차원)에 대해:

\[\hat{\boldsymbol{\beta}} = \arg\min_{\boldsymbol{\beta}} |\mathbf{y} - \mathbf{Z}\boldsymbol{\beta}|_2^2 + \lambda |\boldsymbol{\beta}|_2^2\]

두 임베딩을 비교합니다:

둘 다 같은 총 분산을 가지지만 서로 다른 기하학적 구조를 가집니다.

Lemma 1 (비등방성은 편향을 증가시킨다):

\(\lambda_K > \lambda_1\)일 때, 항상 비등방성 임베딩이 더 큰 편향을 갖는 다운스트림 작업이 존재합니다.

증명의 핵심: Tikhonov 정규화 \(\lambda |\boldsymbol{\beta}|_2^2\)는 최소 고유값에 해당하는 방향(가장 "약한" 방향)에 더 큰 페널티를 줍니다.

비등방적 데이터에서는 일부 방향(고유값 작은 방향)의 정보가 매우 부족하므로, 정규화가 과도하게 그 방향의 가중치를 억제합니다. 이는 실제 타겟이 그 방향을 포함할 때 큰 편향을 만듭니다.

Lemma 2 (비등방성은 분산을 증가시킨다):

정규화 없이(\(\lambda = 0\)) OLS 추정기를 사용할 때:

\[\text{Var}(\hat{\boldsymbol{\beta}}) = \sigma^2 (\mathbf{Z}^T\mathbf{Z})^{-1}\]

추적(trace)을 취하면: \[\text{tr}(\text{Var}(\hat{\boldsymbol{\beta}})) = \sigma^2 \text{tr}((\mathbf{Z}^T\mathbf{Z})^{-1}) = \sigma^2 \sum_{j=1}^K \frac{1}{\lambda_j}\]

핵심 부등식: 고정된 합 \(\sum_j \lambda_j = c\)에 대해, \(\sum_j \frac{1}{\lambda_j}\)를 최소화하려면 모든 \(\lambda_j\)가 같아야 합니다 (코시-슈바르츠 부등식).

따라서 등방성 분포는 분산도 최소화합니다.

2.3 비선형 프로빙: k-NN

선형 프로빙만으로는 충분하지 않습니다. 비선형 평가 방식도 같은 결론을 내릴까요?

k-NN 평가: 쿼리 포인트 \(\mathbf{q}\) 근처의 이웃 \(k\)개 레이블의 평균을 예측합니다.

반지름 기반 k-NN은 더 단순합니다:

\[\hat{y}(\mathbf{q}) = \frac{1}{|\mathcal{N}_{r_0}(\mathbf{q})|} \sum_{n \in \mathcal{N}_{r_0}(\mathbf{q})} y_n\]

기울기 분석: 포인트별 편향을 Taylor 전개로 근사하면:

\[\text{Bias}(\mathbf{q}) = \frac{r_0^2}{d+2}\left(\nabla\eta(\mathbf{q}) \cdot \nabla\log p(\mathbf{q}) + \frac{1}{2}\Delta\eta(\mathbf{q})\right) + O(r_0^4)\]

여기서:

Theorem 1 (k-NN 최적성):

쿼리가 임베딩 분포를 따를 때, 적분 제곱 편향은:

\[\text{ISB}_{k\text{-NN}} = \frac{r_0^4}{(d+2)^2}\tau_g^2 J(p) + O(r_0^4)\]

여기서:

결론: 다운스트림 위험을 최소화하려면 Fisher 정보 \(J(p)\)를 최소화해야 합니다.

Fisher 정보와 가우시안:

Cramér-Rao 부등식에 의해, 위치 패밀리 분포에서: \[J(p) = \text{tr}(\Sigma^{-1})\]

공분산 \(\Sigma\)가 고정 추적을 만족할 때, \(J(p)\)를 최소화하는 유일한 분포는: \[p^* = \mathcal{N}(0, sI_d), \quad s = \text{const}\]

즉, 표준 정규분포(또는 스케일된 등방성 가우시안)입니다.

2.4 가우시안이 특별한 이유

왜 정규분포일까요? 여러 이유가 있습니다:

  1. 최대 엔트로피: 평균과 공분산이 고정되었을 때, 정규분포이 최대 엔트로피를 가집니다.

  2. 안정성: 많은 통계적 성질이 분포 형태에 무관하게 성립합니다.

  3. 계산 편의: 특성함수가 간단하게 표현됩니다.

  4. 선택의 여지 없음: 위의 수학적 분석에서 자연스럽게 도출됩니다.

3. SIGReg: 등방성 가우시안을 강제하는 실제 방법

이제 이론은 명확합니다. 임베딩을 등방성 가우시안 분포로 강제해야 합니다. 그렇다면, 고차원에서 분포 매칭을 어떻게 할까요?

3.1 가설 검정으로 재형식화

표준 거리 메트릭(KL 발산, Wasserstein 거리)은 고차원에서 차원의 저주로 인해 불안정합니다. 대신 통계적 가설 검정 프레임워크를 사용합니다.

\[H_0: P_\theta = Q \quad \text{(귀무가설: 두 분포가 같음)}$$ $$H_1: P_\theta \neq Q \quad \text{(대립가설: 두 분포가 다름)}\]

여기서:

고차원 검정의 어려움: 각 샘플마다 \(d\)개 차원의 정보를 비교해야 하므로, 나이브한 방법은 \(O(d^2)\) 이상의 복잡도를 가집니다.

해결책: Cramér-Wold 정리

모든 1차원 주변분포가 일치하면, 고차원 분포도 일치합니다:

\[P = Q \iff P^{(a)} = Q^{(a)}, \forall \mathbf{a} \in S^{d-1}\]

여기서 \(P^{(a)} = (a^T)_{#} P\)는 방향 \(\mathbf{a}\)로의 푸시포워드(projection)입니다.

따라서 전략:

  1. M개의 랜덤 방향 \({\mathbf{a}_1, ..., \mathbf{a}_M}\) 샘플링
  2. 각 방향에서 1D 테스트 \(T({\mathbf{a}^T f_\theta(\mathbf{x}_n)}_{n=1}^N)\) 수행
  3. 모든 테스트 결과 평균: \(\text{SIGReg} = \frac{1}{|A|}\sum_{\mathbf{a} \in A} T({\mathbf{a}^T f_\theta(\mathbf{x}_n)})\)

3.2 1D 테스트 Epps-Pulley

여러 1D 정규성 테스트가 존재합니다:

1) Moment-based tests (순간 기반):

세 번째와 네 번째 순간으로 정규성을 테스트합니다 (Jarque-Bera):

\[\text{JB} = \frac{N}{6}(\text{skewness}^2 + \text{(kurtosis-3)}^2/4)\]

문제점:

2) CDF-based tests (누적분포 기반):

Cramér-von Mises 또는 Anderson-Darling:

\[T_w = \int_{-\infty}^{\infty} (F_N(x) - F(x))^2 w(x) dF(x)\]

문제점:

3) Characteristic Function-based tests (특성함수 기반):

Epps-Pulley 테스트:

\[EP = N \int_{-\infty}^{\infty} |\hat{\phi}_X(t) - \phi(t)|^2 w(t) dt\]

여기서:

장점:

  1. 자동 미분 가능: 복소 지수는 매끄럽게 미분 가능

  2. 경계진 기울기: Theorem 4에 의해 \[\left|\frac{\partial EP}{\partial X_i}\right| \leq \frac{4\sigma^2}{N}\] 기울기가 샘플 수에만 의존, 분포 형태 무관

  3. 경계진 곡률: 2차 도함수도 유계

  4. 효율적 분산 훈련: 모든 all-reduce 연산

  5. 단순 구현: PyTorch에서 몇 줄로 구현 가능

3.3 고차원 저주 극복

M개 방향만으로 정말 충분할까요? 고차원 공간 속 구면(sphere) 위에 고르게 분포된 M개 점으로 매끄러운 함수를 충분히 표현할 수 있다면 가능합니다.

Theorem 5 (오차 경계)

Sobolev 평활성 \(\alpha \in H^\alpha(\mathbb{R}^d)\)인 임베딩에 대해:

\[\mathbb{E}_{\mathbf{a}}\left[\int_{\mathbb{R}} |\varphi_\mathbf{a}(t) - \varphi_{\mathcal{N}}(t)|^2 dt\right] \leq C(d,\alpha)|A|^{-2\alpha/(d-1)} \cdot (\text{범위})\]

직관:

실제 관찰:

3.4 PyTorch 구현

def SIGReg(x, global_step, num_slices=256):
    # x: (N, K) - 임베딩
    # global_step: 동기화용
    # num_slices: M (방향 개수)
    
    # 1. 동기화된 방향 생성
    generator = torch.Generator(device=x.device)
    generator.manual_seed(global_step)
    
    proj_shape = (x.size(1), num_slices)
    A = torch.randn(proj_shape, generator=generator, device=x.device)
    A /= A.norm(p=2, dim=0)  # 단위 벡터로 정규화
    
    # 2. 특성함수 적분점
    t = torch.linspace(-5, 5, 17, device=x.device)
    exp_f = torch.exp(-0.5 * t**2)  # N(0,1)의 특성함수
    
    # 3. 경험적 특성함수 계산
    x_t = x.unsqueeze(2) * t  # (N, K, 17)
    ecf = (1j * x_t).exp().mean(0)  # (K, 17)
    ecf = torch.distributed.all_reduce(ecf) / world_size  # DDP 동기화
    
    # 4. Epps-Pulley 통계
    err = (ecf - exp_f).abs().square() * exp_f
    T = torch.trapz(err, t, dim=1)  # (K,)
    
    N = x.size(0) * world_size
    return T.mean() * N

전체 LeJEPA 손실:

def lejepa_loss(global_views, all_views, lambda_param):
    # 글로벌 뷰: (2, Bs, K)
    # 모든 뷰: (8, Bs, K)
    
    # 글로벌 뷰의 평균
    centers = global_views.mean(0)  # (Bs, K)
    
    # 예측 손실
    pred_loss = (centers - all_views).square().mean()
    
    # SIGReg 손실 (모든 뷰에 적용)
    sigreg_loss = all_views.reshape(-1, K).new_tensor(0.)
    for view_emb in all_views:
        sigreg_loss = sigreg_loss + SIGReg(view_emb, global_step)
    sigreg_loss = sigreg_loss / all_views.size(0)
    
    total_loss = (1 - lambda_param) * pred_loss + lambda_param * sigreg_loss
    return total_loss

4. 실험

4.1 안정성: 하이퍼파라미터 불변성

테스트 1: λ (trade-off 파라미터) 변화

ImageNet-1K에서 ViT-Large/14, 100 에포크 학습 후 선형 프로빙:

λ

정확도

0.01

72.88%

0.02

74.68%

0.04

73.71%

0.05

75.02%

0.08

74.50%

0.10

74.50%

결론: λ 선택에 강건함. 기본값 0.05에서 최고 성능이지만, 전체 범위에서 안정적입니다.

테스트 2: 배치 크기

BS

정확도

128

72.20%

256

74.15%

512

74.72%

1024

74.07%

결론: 매우 작은 배치(BS=128)에서도 작동. 기존 방법들은 보통 BS≥256 필요.

테스트 3: 뷰 개수 (V_g: 글로벌, V_l: 로컬)

V_g

V_l

정확도

4

1

53.06%

4

2

72.26%

4

4

73.68%

2

8

75.08%

1

10

74.06%

결론: 전형적 설정(V_g=2, V_l=8)이 최적이지만, 다양한 구성에서 견고합니다.

4.2 훈련 손실과 성능의 놀라운 상관관계

자기 지도 학습의 오래된 문제: 훈련 손실이 모델 품질을 나타내는가?

기존 JEPA/DINO에서는 훈련 손실과 성능이 약한 상관관계를 보였습니다. 이는 레이블 없이 모델 선택이 어렵다는 뜻입니다.

LeJEPA의 발견:

Spearman 상관계수 (ImageNet-1K, ViT-base):
94.52% (λ=0.05 기본)
→ 99% (스케일 보정 후)

이는 놀랍습니다. 훈련 손실만으로 다운스트림 성능을 거의 완벽하게 예측할 수 있다는 의미입니다.

스케일 법칙:

상관계수를 최적화하는 간단한 스케일링:

\[C(\alpha) = \rho_s\!\left(\frac{\text{train\_loss}}{\lambda^\alpha},\, \text{test\_accuracy}\right)\]

\(\alpha \approx 0.4\)일 때 최대 상관계수 99% 달성.

실무적 의미: 레이블 없이 모델 선택이 가능합니다!

4.3 인도메인 프리트레이닝

기존 패러다임: 대형 데이터(ImageNet)로 프리트레이닝 → 특수 도메인 전이학습

새로운 발견: 작은 도메인에서도 LeJEPA로 인도메인 프리트레이닝이 전이학습을 능가합니다.

Galaxy10 데이터셋 (11,000 샘플, 10개 클래스):

모델

설정

전체

100샘플

10샘플

LeJEPA ConvNext-V2-Nano (14M)

인도메인

82.72%

75.34%

59.85%

LeJEPA ResNet-34 (21M)

인도메인

83.28%

74.93%

53.95%

DINOv2 ViT-S (21M)

전이

78.34%

60.81%

36.23%

DINOv3 ViT-S (21M)

전이

81.60%

69.87%

44.71%

차이 분석:

이유

  1. 도메인 시프트: Galaxy10은 천문학 이미지 (자연 이미지와 거리 멀음)
  2. 깔끔한 최적화: LeJEPA의 이론적 최적성이 도메인 특수성을 더 잘 활용
  3. 하이퍼파라미터 안정성: λ=0.05 기본값만으로 충분

4.4 대규모 확장

ViT-gigantic (1.8B 파라미터), ImageNet-1K:

핵심 관찰:

이는 수학적 최적성이 스케일에서도 유지됨을 시사합니다.

4.5 레이블 없는 객체 분할

흥미로운 부가 발견: LeJEPA는 명시적 감독 없이 의미 있는 객체 경계를 학습합니다.

방법:

  1. ViT의 마지막 층 주의 맵(attention map) 추출
  2. [CLS] 토큰의 주의 점수에 임계값 적용
  3. 결과 마스크가 객체 분할로 기능

시각화 결과:

이는 DINO도 보였던 현상이지만, LeJEPA에서도 자연스럽게 나타납니다.

비판적 평가 및 한계

강점

  1. 수학적 견고성: 등방성 가우시안의 최적성 증명이 명확하고 엄밀함
  2. 구현 단순성: 50줄 코드로 기존 복잡한 시스템 대체 가능
  3. 광범위한 적용성: 60개 이상 아키텍처에서 하이퍼파라미터 조정 불필요
  4. 이론-실무 일치: 수학적 예측이 실험에서 확인됨

고려사항

1. 이론의 범위 제한:

2. 절대 성능:

3. 실험 범위:

4. 계산 오버헤드:

5. 가정의 현실성:

결론

LeJEPA는 이론과 실무의 아름다운 만남입니다.

자기 지도 학습이 수십 개의 임시방편으로 복잡해진 상황에서, 저자들은 단순한 수학적 원리로 이를 환원시켰습니다. 더욱 놀라운 점은:

  1. 이론이 명확하고 검증 가능함
  2. 구현이 간단하고 투명함
  3. 성능이 기존 방법과 경쟁력 있음
  4. 모든 설정에서 안정적으로 작동함

적용 시나리오

LeJEPA의 강점

기존 방법의 강점

이 논문은 중요한 메시지를 전합니다:

"더 많은 휴리스틱이 항상 답이 아니다. 때로는 문제를 다시 정의하면 더 간단한 해결책이 있다."

이는 머신러닝 연구의 방향성에 시사점을 줍니다.

참고자료