Diffusion Transformers with Representation Autoencoders

B. Zheng, N. Ma, S. Tong and S. Xie, "Diffusion Transformers with Representation Autoencoders", Preprint, 2025, DOI: 10.48550/arXiv.2510.11690.

최근 이미지 생성 분야에서 Diffusion Transformer(DiT)는 픽셀 공간이 아닌 사전 학습된 오토인코더가 만든 잠재 공간(latent space)에서 확산 과정을 수행하는 것이 표준이 되었습니다. 하지만 대부분의 DiT는 여전히 원래의 VAE 인코더에 의존하고 있고, 이는 몇 가지 한계를 가지고 있습니다. 이 논문은 VAE를 사전 학습된 표현 인코더(DINO, SigLIP, MAE 등)와 학습된 디코더로 구성된 Representation Autoencoder(RAE)로 대체하는 새로운 접근을 제안합니다.

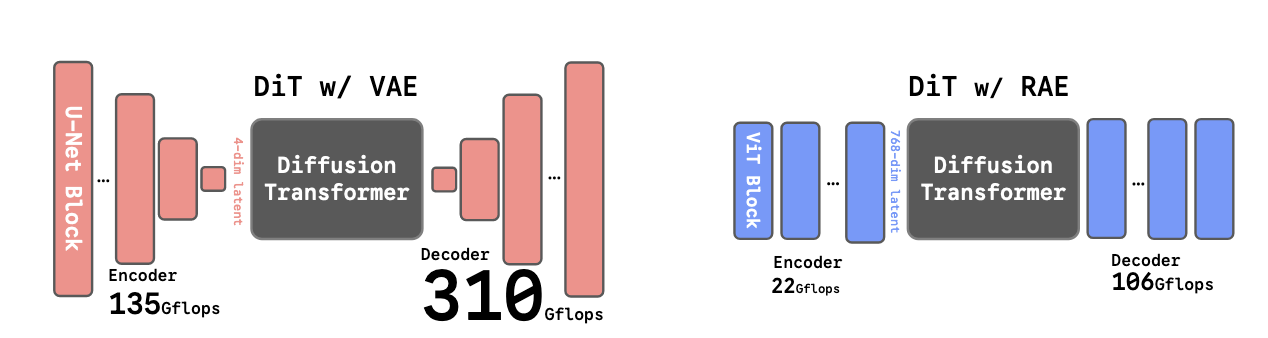
요약

아키텍처: RAE는 동결된(frozen) 사전 학습 표현 인코더와 경량 ViT 기반 디코더로 구성됩니다. DiT에는 표준 DiT 백본에 얕지만 넓은 DDT head를 추가한 DiTDH 변형이 사용됩니다.

사용 모델: DINOv2, SigLIP2, MAE와 같은 사전 학습된 표현 인코더를 사용하며, 특히 DINOv2-B가 생성 작업에서 가장 좋은 성능을 보였습니다.

데이터셋: ImageNet-1K를 사용하여 256×256 및 512×512 해상도에서 학습 및 평가를 수행했습니다.

평가 매트릭: FID(Fréchet Inception Distance), IS(Inception Score), Precision, Recall을 사용하여 생성 품질을 평가했습니다. 재구성 품질은 rFID(reconstruction FID)로 측정했습니다.

훈련 방법: Flow matching 목적 함수를 사용하며, 선형 보간 \(x_t = (1-t)x + t\epsilon\)을 통해 노이즈와 깨끗한 데이터를 혼합합니다. 모델은 속도 \(v(x_t, t)\)를 예측하도록 학습됩니다. 주요 기법으로는 (1) 토큰 차원에 맞춘 DiT 너비 조정, (2) 차원 의존적 노이즈 스케줄 시프트, (3) 노이즈 증강 디코더 학습이 있습니다.

주요 결과: ImageNet 256×256에서 가이던스 없이 FID 1.51, AutoGuidance 사용 시 FID 1.13을 달성했습니다. 512×512 해상도에서도 가이던스 사용 시 FID 1.13을 기록했습니다.

논문 상세

Introduction

생성 모델의 발전은 데이터 표현을 학습하는 방식의 지속적인 재정의를 통해 이루어져 왔습니다. 초기 픽셀 공간 모델은 이미지 통계를 직접 캡처하려 했지만, latent diffusion의 등장으로 생성 과정은 학습된 압축 표현 공간에서 작동하도록 재구성되었습니다. LDM이나 DiT 같은 모델들은 이 공간에서 확산 과정을 수행하여 더 높은 시각적 품질과 효율성을 달성했습니다.

하지만 확산 백본의 발전에도 불구하고, 잠재 공간을 정의하는 오토인코더는 거의 변하지 않았습니다. 널리 사용되는 SD-VAE는 여전히 무거운 채널 압축과 재구성 전용 목적 함수에 의존하며, 전역 의미 구조가 부족한 저용량 잠재 표현을 생성합니다.

한편, 시각적 표현 학습은 급격한 변화를 겪었습니다. DINO, MAE, CLIP/SigLIP 같은 자기 지도 및 다중 모달 인코더는 의미론적으로 구조화된 시각적 특징을 학습하여 여러 작업과 규모에서 일반화됩니다. 그러나 latent diffusion은 이러한 발전과 대체로 격리되어 있으며, 의미론적으로 의미 있는 표현 공간이 아닌 재구성 학습된 VAE 공간에서 확산을 계속하고 있습니다.

이 분리는 의미론적 목적과 생성적 목적 간의 비호환성에 대한 오래된 가정에서 비롯됩니다. 의미론을 캡처하도록 학습된 인코더는 충실한 재구성에 적합하지 않다고 널리 믿어지고 있으며, 확산 모델이 고차원 잠재 공간에서는 성능이 떨어진다고 여겨집니다.

이 논문에서는 두 가정이 모두 틀렸을 수 있음을 보입니다. 동결된 표현 인코더도, 의미론을 위해 명시적으로 최적화된 인코더도 아키텍처 복잡성이나 보조 손실 없이 SD-VAE보다 우수한 재구성을 제공하는 강력한 오토인코더로 재활용될 수 있음을 보여줍니다.

Related Work

표현과 재구성: 최근 연구는 의미론적 표현으로 VAE를 강화하는 것을 탐구합니다. VA-VAE는 VAE 잠재 표현을 사전 학습된 표현 인코더와 정렬하고, MAETok, DC-AE 1.5, l-DEtok은 VAE 학습에 MAE 또는 DAE 영감의 목적을 통합합니다. 이러한 정렬은 VAE의 재구성 및 생성 성능을 크게 향상시키지만, 심하게 압축된 저차원 잠재 표현에 대한 의존은 재구성 충실도와 표현 품질을 모두 제한합니다.

표현과 생성: REPA는 중간 블록을 표현 인코더 특징과 정렬하여 DiT 수렴을 가속화합니다. DDT는 DiT를 인코더-디코더로 분리하고 인코더 출력에 REPA 손실을 적용하여 수렴을 더욱 개선합니다. REG는 DiT 시퀀스에 학습 가능한 토큰을 도입하고 이를 표현 인코더 표현과 명시적으로 정렬합니다.

High Fidelity Reconstruction from Frozen Encoders

이 섹션에서는 DINOv2나 SigLIP2 같은 사전 학습된 표현 인코더가 "고수준 의미론을 강조하면서 저수준 세부 사항을 경시"하기 때문에 재구성 작업에 적합하지 않다는 일반적인 가정에 도전합니다.

RAE 학습 방법: 입력 \(x \in \mathbb{R}^{3 \times H \times W}\)와 동결된 표현 인코더 \(E\)(패치 크기 \(p_e\), 은닉 크기 \(d\))가 주어지면, \(N = HW/p_e^2\)개의 토큰을 \(d\) 채널로 얻습니다. ViT 디코더 \(D\)(패치 크기 \(p_d\))는 이들을 \(3 \times H\frac{p_d}{p_e} \times W\frac{p_d}{p_e}\) 형태의 픽셀로 다시 매핑합니다.

디코더 \(D\)는 L1, LPIPS, 적대적 손실의 조합으로 학습됩니다:

\[z = E(x), \quad \hat{x} = D(z)\]

\[L_{rec}(x) = \omega_L \text{LPIPS}(\hat{x}, x) + \text{L1}(\hat{x}, x) + \omega_G \lambda \text{GAN}(\hat{x}, x)\]

실험 결과: DINOv2-B, SigLIP2-B, MAE-B를 포함한 세 가지 대표적인 인코더를 선택했습니다. 모든 RAE는 동결된 인코더를 사용하여 SD-VAE보다 일관되게 더 나은 재구성 품질(rFID)을 달성합니다. 특히 MAE-B/16을 사용한 RAE는 rFID 0.16을 달성하여 SD-VAE를 명확히 능가합니다.

디코더 용량을 늘리면(ViT-B에서 ViT-XL로) rFID가 일관되게 향상됩니다: 0.58에서 0.49로. 중요한 것은 ViT-B가 이미 SD-VAE를 능가하면서도 GFLOPs에서 14배 더 효율적이라는 점입니다.

표현 품질의 경우, RAE는 동결된 사전 학습 인코더를 사용하므로 기본 표현 인코더의 표현을 직접 상속받습니다. 선형 프로빙을 통한 평가에서 DINOv2-B는 84.5% 정확도를 달성한 반면, SD-VAE는 약 8% 정확도만 달성했습니다.

Taming Diffusion Transformers for RAE

RAE가 좋은 재구성 품질을 보여주었으므로, 이제 잠재 공간의 확산 가능성(diffusability), 즉 확산 모델이 잠재 분포를 얼마나 쉽게 모델링할 수 있는지, 그리고 생성 성능이 얼마나 좋은지를 조사합니다.

표준 DiT가 작동하지 않음: 표준 확산 레시피는 RAE와 함께 실패합니다. RAE 잠재 표현에서 직접 학습하면 DiT-S 같은 작은 백본은 완전히 실패하고, DiT-XL 같은 더 큰 백본도 SD-VAE 잠재 표현을 사용하는 대응 모델보다 훨씬 성능이 떨어집니다.

DiT 너비를 토큰 차원에 맞추기

단일 이미지로 오버피팅하는 간단한 실험을 구성했습니다. 깊이를 고정하고 모델 너비를 변경하면, 모델 너비 \(d <\) 토큰 차원 \(n = 768\)일 때 샘플 품질이 나쁘지만, \(d \geq n\)이 되면 급격히 개선되어 입력을 거의 완벽하게 재현합니다.

이것이 여전히 더 큰 모델 용량에서 비롯된 것인지 확인하기 위해 너비를 \(d = 384\)로 고정하고 깊이를 변경했습니다. 깊이를 12에서 24로 두 배로 늘려도 생성된 이미지는 여전히 아티팩트가 많고 학습 손실이 유사한 수준으로 수렴하지 못했습니다.

이 결과는 RAE의 잠재 공간에서 생성이 성공하려면 확산 모델의 너비가 RAE의 토큰 차원과 일치하거나 초과해야 함을 나타냅니다.

이론적 정당화 (Theorem 1): \(x \sim p(x) \in \mathbb{R}^n\), \(\epsilon \sim N(0, I_n)\), \(t \in [0,1]\)이라 가정합니다. \(x_t = (1-t)x + t\epsilon\)일 때, 함수군

\[G_d = {g(x_t, t) = Bf(Ax_t, t) : A \in \mathbb{R}^{d \times n}, B \in \mathbb{R}^{n \times d}, f : [0,1] \times \mathbb{R}^d \to \mathbb{R}^d}\]

에서 \(d < n\)인 경우, 모든 \(g \in G_d\)에 대해

\[L(g, \theta) = \int_0^1 \mathbb{E}_{x \sim p(x), \epsilon \sim N(0, I_n)}[|g(x_t, t) - (\epsilon - x)|^2]dt \geq \sum_{i=d+1}^n \lambda_i\]

여기서 \(\lambda_i\)는 확률 변수 \(W = \epsilon - x\)의 공분산 행렬의 고유값입니다.

\(d \geq n\)일 때, \(G_d\)는 \(L(g, \theta)\)의 유일한 최소화자를 포함합니다.

차원 의존적 노이즈 스케줄 시프트

많은 선행 연구에서 입력 \(z \in \mathbb{R}^{C \times H \times W}\)에 대해 공간 해상도(\(H \times W\))를 높이면 동일한 노이즈 수준에서 정보 손상이 감소하여 확산 학습이 손상된다는 것을 관찰했습니다. 이러한 발견은 주로 채널이 적은(\(C \leq 16\)) 픽셀 또는 VAE 인코딩 입력을 기반으로 합니다.

가우시안 노이즈는 공간 및 채널 차원 모두에 적용되므로, 채널 수가 증가하면 토큰당 유효 "해상도"도 증가하여 정보 손상이 더욱 감소합니다. 따라서 이러한 선행 연구에서 제안된 해상도 의존 전략은 토큰 수와 차원의 곱으로 정의되는 유효 데이터 차원으로 일반화되어야 한다고 주장합니다.

Esser et al. (2024)의 시프팅 전략을 채택합니다: 스케줄 \(t_n \in [0,1]\)과 입력 차원 \(n, m\)에 대해, 시프트된 타임스텝은 \(t_m = \frac{\alpha t_n}{1 + (\alpha - 1)t_n}\)로 정의되며, 여기서 \(\alpha = \sqrt{m/n}\)는 차원 의존 스케일링 인자입니다.

실험 결과, 이는 상당한 성능 향상을 가져와 고차원 RAE 잠재 공간에서 확산 모델을 학습하는 데 중요함을 보여줍니다. 시프트를 적용하지 않으면 gFID가 23.08이지만, 적용하면 4.81로 크게 개선됩니다.

노이즈 증강 디코딩

VAE와 달리 잠재 토큰이 연속 분포 \(N(\mu, \sigma^2 I)\)로 인코딩되는 경우, RAE 디코더 \(D\)는 이산 분포 \(p(z) = \sum_i \delta(x - z_i)\)에서 이미지를 재구성하도록 학습됩니다.

그러나 추론 시 확산 모델은 불완전한 학습 및 샘플링으로 인해 노이즈가 있거나 학습 분포에서 약간 벗어난 잠재 표현을 생성할 수 있습니다. 이는 \(D\)에 상당한 out-of-distribution 문제를 야기할 수 있습니다.

이 문제를 완화하기 위해 가산 노이즈 \(n \sim N(0, \sigma^2 I)\)로 RAE 디코더 학습을 증강합니다. 깨끗한 잠재 분포 \(p(z)\)에서 직접 디코딩하는 대신, 스무드된 분포 \(p_n(z) = \int p(z-n)N(0, \sigma^2 I)(n)dn\)에서 \(D\)를 학습하여 확산 모델의 더 조밀한 출력 공간에 대한 디코더의 일반화를 향상시킵니다.

\(p_n(z)\)를 사용하면 gFID가 4.81에서 4.28로 개선되지만 rFID는 0.49에서 0.57로 약간 악화됩니다. 이 트레이드오프는 예상된 것입니다: 노이즈를 추가하면 잠재 분포가 부드러워지므로 디코더의 OOD 문제를 줄이는 데 도움이 되지만, 미세한 디테일도 제거되어 재구성 품질이 낮아집니다.

Improving Model Scalability with Wide Diffusion Head

표준 DiT 프레임워크 내에서 고차원 RAE 잠재 표현을 처리하려면 전체 백본의 너비를 확장해야 하며, 이는 빠르게 계산 비용이 많이 듭니다. 이 한계를 극복하기 위해 DDT에서 영감을 받아 디노이징 전용의 얕지만 넓은 트랜스포머 모듈인 DDT head를 도입합니다.

Wide DDT head: 공식적으로 DiTDH 모델은 기본 DiT \(M\)과 추가적인 넓고 얕은 트랜스포머 헤드 \(H\)로 구성됩니다. 노이즈가 있는 입력 \(x_t\), 타임스텝 \(t\), 선택적 클래스 레이블 \(y\)가 주어지면, 결합된 모델은 속도 \(v_t\)를 다음과 같이 예측합니다:

\[z_t = M(x_t | t, y)$$ $$v_t = H(x_t | z_t, t)\]

DiTDH의 빠른 수렴: DiTDH는 DiT보다 훨씬 더 FLOP 효율적입니다. 예를 들어, DiTDH-B는 학습 FLOP의 약 40%만 필요하지만 DiT-XL을 큰 차이로 능가합니다. 비슷한 학습 예산에서 DiTDH-XL로 확장하면 FID 2.16을 달성하여 DiT-XL의 거의 절반입니다.

다양한 RAE 규모에서의 우수성: DiTDH-XL과 DiT-XL을 세 가지 RAE 인코더(DINOv2-S, B, L)에서 비교했습니다. DiTDH는 일관되게 DiT를 능가하며, 인코더 크기가 커질수록 이점이 커집니다. 예를 들어 DINOv2-L을 사용하면 DiTDH가 FID를 6.09에서 2.73으로 개선합니다.

State-of-the-Art Results

수렴 속도: DiTDH-XL은 REPA-XL, MDTv2-XL, SiT-XL을 약 \(5 \times 10^{10}\) GFLOPs 근처에서 이미 능가하며, \(5 \times 10^{11}\) GFLOPs에서 전체적으로 최고의 FID를 달성하는데, 이는 40배 이상 적은 계산량입니다.

확장성: DiTDH의 크기를 늘리면 FID 점수가 일관되게 향상됩니다. 가장 작은 모델인 DiTDH-S는 경쟁력 있는 FID 6.07을 달성하여 훨씬 큰 REPA-XL을 이미 능가합니다. DiTDH-S에서 DiTDH-B로 확장하면 FID가 6.07에서 3.38로 크게 개선되어 비슷하거나 더 큰 규모의 모든 선행 연구를 능가합니다.

성능: ImageNet 256×256에서 DiTDH-XL은 가이던스 없이 FID 1.51, 가이던스 사용 시 FID 1.13의 새로운 최고 수준을 설정했습니다. 512×512에서는 400 에폭 학습으로 가이던스 사용 시 FID 1.13을 달성하여 EDM-2의 이전 최고 성능(1.25)을 능가했습니다.

Discussions

고해상도 합성: 해상도 확장을 처리하기 위해 디코더의 패치 크기 \(p_d\)가 인코더 패치 크기 \(p_e\)와 다르도록 허용합니다. \(p_d = 2p_e\)로 설정하면 256×256에서 사용된 것과 동일한 토큰에서 512×512 이미지를 재구성하는 2배 업샘플링 이미지가 생성됩니다. 256×256 해상도에서 학습된 확산 모델을 재사용하고 업샘플링 디코더로 교체하여 재학습 없이 512×512 출력을 생성할 수 있습니다.

VAE 없이 DiTDH: DiTDH-XL을 SD-VAE 잠재 표현에서 학습하면 DiT-XL보다 성능이 더 나빠집니다(gFID 7.13 대 11.70). 이는 DDT head가 저차원 잠재 공간에서는 거의 이점을 제공하지 않으며, 주요 강점이 RAE가 도입한 고차원 확산 작업에서 발생함을 나타냅니다.

구조화된 표현의 역할: 픽셀에서 DiTDH가 DiT를 능가하지만, 두 모델 모두 RAE 잠재 표현에서 학습된 대응 모델보다 훨씬 성능이 나쁩니다(픽셀의 DiTDH gFID 30.56 대 DINOv2-B의 2.16). 이러한 결과는 고차원성만으로는 충분하지 않음을 보여줍니다: RAE가 제공하는 구조화된 표현이 강력한 성능 향상을 달성하는 데 중요합니다.

Conclusion

이 연구에서는 사전 학습된 표현 인코더가 재구성이나 생성에 너무 고차원적이고 의미론적이라는 믿음에 도전합니다. 동결된 표현 인코더를 경량 학습 디코더와 결합하면 효과적인 Representation Autoencoder(RAE)를 형성한다는 것을 보여줍니다. 이 잠재 공간에서 세 가지 추가 구성 요소를 통해 Diffusion Transformer를 안정적이고 효율적으로 학습할 수 있습니다: (1) DiT 너비를 인코더 토큰 차원에 맞추기, (2) 노이즈 스케줄에 차원 의존 시프트 적용, (3) 디코더 노이즈 증강. 또한 얕지만 넓은 확산 트랜스포머 헤드인 DiTDH를 도입하여 2차 계산 없이 너비를 증가시킵니다.

경험적으로 RAE는 강력한 시각적 생성을 가능하게 합니다: ImageNet에서 RAE 기반 DiTDH-XL은 256×256에서 FID 1.51(가이던스 없음), 256×256 및 512×512 모두에서 FID 1.13(가이던스 사용)을 달성합니다. RAE 잠재 표현은 향후 확산 트랜스포머 학습을 위한 강력한 후보 역할을 한다고 생각합니다.