Deep Delta Learning

심층 신경망의 학습 안정성을 책임지는 ResNet의 identity shortcut connection은 사실 너무 단순하다는 문제가 있습니다. 입력에 residual을 더하는 방식은 기울기 소실 문제는 해결했지만, 네트워크가 복잡한 상태 전이를 표현하는 데는 한계가 있었죠. 새로운 논문 Deep Delta Learning(DDL)은 이 shortcut 연결에 학습 가능한 기하학적 변환을 추가해서, 네트워크가 identity mapping, 직교 투영(orthogonal projection), 그리고 기하학적 반사(geometric reflection)를 동적으로 선택할 수 있도록 만듭니다. 핵심은 단 하나의 스칼라 게이트 \(\beta(X)\)로 이 모든 변환을 제어한다는 점입니다.

논문 정보

제목: Deep Delta Learning
저자: Y. Zhang, Y. Liu, M. Wang, and Q. Gu
소속: Princeton University, University of California, Los Angeles
발행: arXiv preprint, 2026-01-01
DOI: 10.48550/arXiv.2601.00417
인용: Y. Zhang, Y. Liu, M. Wang, and Q. Gu, "Deep Delta Learning," arXiv preprint arXiv:2601.00417, 2026.

ResNet이 등장한 지 거의 10년이 지났습니다. 그동안 identity shortcut connection은 심층 신경망의 학습 안정성을 책임지는 사실상의 표준이 되었죠. 하지만 이 구조는 근본적으로 "덧셈"만 할 수 있습니다. \(X_{l+1} = X_l + F(X_l)\) 형태의 업데이트는 기울기 소실 문제를 해결하긴 했지만, 네트워크가 배울 수 있는 동역학(dynamics)에 강한 제약을 겁니다. 특히 진동(oscillation)이나 대립적 행동(oppositional behavior) 같은 복잡한 패턴을 모델링하려면 음의 고유값(negative eigenvalue)을 가진 변환이 필요한데, 순수한 덧셈 구조로는 이게 불가능합니다.

프린스턴 대학교와 UCLA의 연구팀이 제안한 Deep Delta Learning은 이 문제를 정면으로 다룹니다. 저자들은 Householder 반사라는 수치 선형대수의 고전적 도구를 신경망 구조에 접목시켜, identity shortcut을 학습 가능한 기하학적 변환으로 일반화했습니다. 핵심 아이디어는 단순합니다: shortcut 연결에 rank-1 변환을 적용하되, 그 강도를 데이터에 따라 동적으로 조절하는 것이죠. 이렇게 하면 네트워크는 층마다 "그냥 넘어갈지", "특정 방향의 정보를 지울지", "완전히 반사시킬지"를 스스로 결정할 수 있게 됩니다.

요약

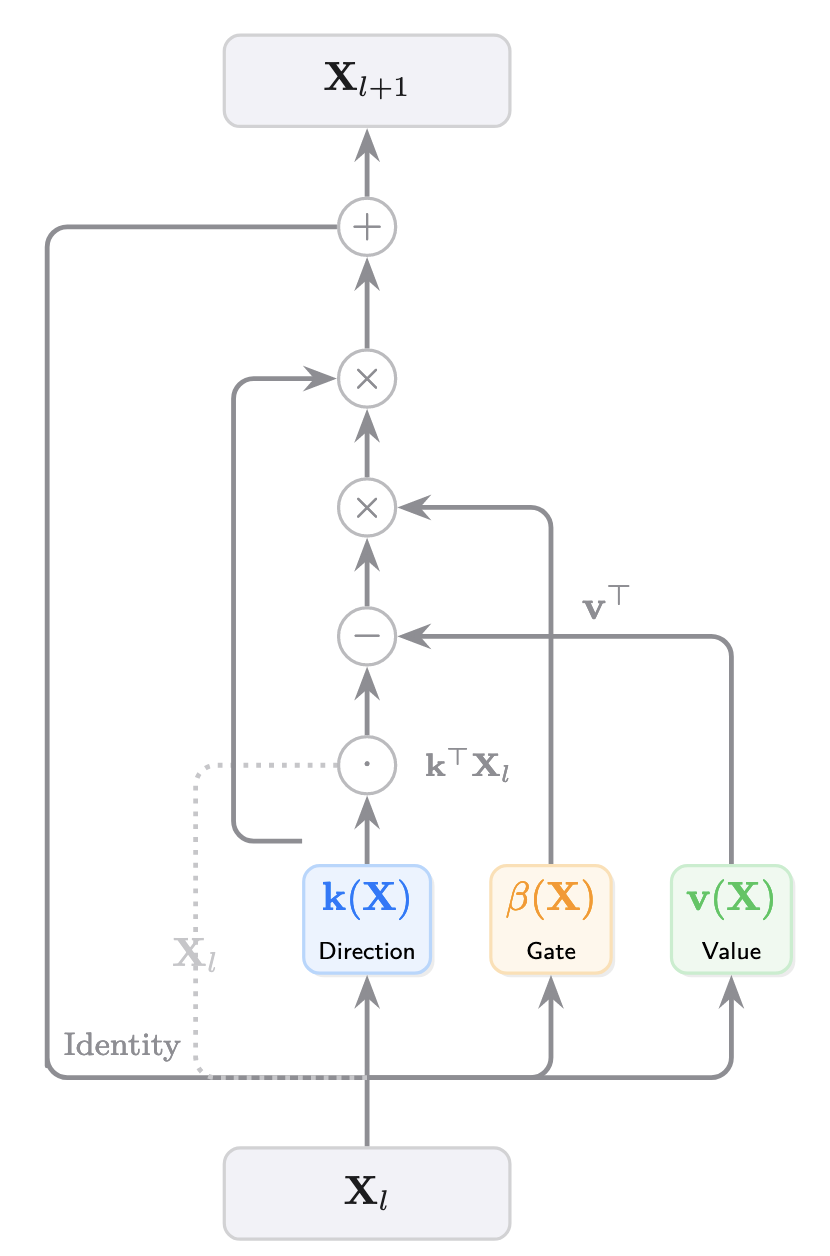Deep Delta Learning은 기존 residual block의 identity shortcut에 **Delta Operator**라는 rank-1 기하학적 변환을 추가합니다:

\[ X_{l+1} = A(X_l)X_l + \beta(X_l)k(X_l)v(X_l)^\top \]

여기서:

\(A(X) = I - \beta(X)k(X)k(X)^\top\): Delta Operator (shortcut 변환)
\(k(X) \in \mathbb{R}^d\): 학습된 반사 방향 벡터 (단위 벡터)
\(\beta(X) \in [0, 2]\): 학습된 스칼라 게이트
\(v(X) \in \mathbb{R}^{d_v}\): residual value 벡터

기하학적 해석

\(\beta\)의 값에 따라 연산자가 다르게 동작합니다:

\(\beta\) 값	고유값	기하학적 의미	행렬식
\(\beta \to 0\)	\((1, 1, ..., 1)\)	Identity mapping	\(\det(A) = 1\)
\(\beta \to 1\)	\((0, 1, ..., 1)\)	Orthogonal projection	\(\det(A) = 0\)
\(\beta \to 2\)	\((-1, 1, ..., 1)\)	Householder reflection	\(\det(A) = -1\)

주요 특성

스펙트럼 제어: 단 하나의 스칼라 \(\beta\)로 변환의 고유값 구조를 완전히 제어
Delta Rule 통합: depth 차원에서 Delta Rule을 구현 (\(v^\top - k^\top X\) 형태의 오차 신호)
연속적 보간: identity, projection, reflection 사이를 미분 가능하게 전환
동기화된 삭제/쓰기: 같은 \(\beta\)로 정보 삭제(erasure)와 주입(injection)을 동시에 제어

실험 설정

구현 방식: MLP 기반 또는 Attention 기반 파라미터화
정규화: \(k\)는 \(L_2\) 정규화로 단위 벡터로 제한
게이트 범위: \(\beta(X) = 2 \cdot \sigma(\text{Linear}(G(X)))\)로 \([0, 2]\) 범위 보장
수치 안정성: \(\epsilon > 0\)을 추가하여 \(k^\top k + \epsilon\)으로 나눔

논문 상세

1. 서론: Residual Connection의 한계

심층 residual 네트워크의 효율성은 근본적으로 identity shortcut connection에 달려 있습니다. 이 메커니즘은 기울기 소실 문제를 효과적으로 완화하지만, 동시에 feature 변환에 "엄격한 덧셈 귀납 편향(strictly additive inductive bias)"을 부과합니다.

표준 ResNet의 업데이트 규칙을 보면:

\[ X_{l+1} = X_l + F(X_l) \]

이는 ODE \(\dot{X} = F(X)\)에 대한 forward Euler step(step size 1)으로 볼 수 있습니다. 이 관점은 심층 네트워크를 동역학계(dynamical system)와 연결시켜주죠. 하지만 문제가 있습니다. 엄격한 덧셈 업데이트는 학습된 동역학에 강한 translation bias를 걸어놓습니다. shortcut path는 항상 identity operator와 같은 고정된 Jacobian을 유지하니까요.

이 강직성(rigidity)은 네트워크가 표현할 수 있는 상태 전이를 제한합니다. 최근 연구(Grazzi et al., 2024)는 진동이나 대립적 행동 같은 패턴을 모델링하려면 음의 고유값을 갖는 변환이 필요하다는 점을 지적했습니다. 하지만 순수한 덧셈 구조로는 이게 불가능합니다.

2. Delta Residual Block: 수학적 기초

저자들은 이 한계를 극복하기 위해 기하학적 선형대수에 뿌리를 둔 원리적 일반화를 제안합니다. 그 출발점은 Householder 변환입니다.

2.1 Householder 행렬

영벡터가 아닌 벡터 \(k \in \mathbb{R}^d\)에 대해, Householder 행렬 \(H_k\)는 다음과 같이 정의됩니다:

\[ H_k = I - 2\frac{kk^\top}{|k|_2^2} \]

기하학적으로 \(H_k\)는 법선 벡터가 \(k\)인 초평면에 대해 벡터를 반사시킵니다. 이 행렬은 수치 선형대수의 핵심 도구로, 여러 중요한 성질을 가집니다:

대칭성: \(H_k = H_k^\top\)
직교성: \(H_k^\top H_k = I\) (길이 보존)
대합성: \(H_k^2 = I\) (두 번 반사하면 원점)

스펙트럼 관점에서 보면, \(H_k\)는 고유값 \(-1\)을 하나 가지고 (고유벡터 \(k\)), 나머지 \(d-1\)개는 고유값 \(1\)입니다 (고유공간 \(k^\perp\)).

2.2 Delta Operator의 정의

DDL의 핵심 아이디어는 Householder 행렬의 상수 인자 2를 학습 가능한 데이터 의존적 스칼라 게이트 \(\beta(X)\)로 교체하는 것입니다.

hidden state를 행렬 \(X \in \mathbb{R}^{d \times d_v}\)로 표현합니다. 여기서 \(d\)는 feature 차원, \(d_v\)는 value 채널의 개수입니다. DDL block의 출력은:

\[ X_{l+1} = A(X_l)X_l + \beta(X_l)k(X_l)v(X_l)^\top \]

여기서 \(v \in \mathbb{R}^{d_v}\)는 branch \(F: \mathbb{R}^{d \times d_v} \to \mathbb{R}^{d_v}\)가 생성한 residual value 벡터입니다. outer product \(kv^\top\)이 덧셈 업데이트를 구성합니다. 중요한 점은 게이트 \(\beta(X)\)를 이 생성(constructive) 항에도 적용한다는 것입니다. 이렇게 하면 삭제(erasure)와 쓰기(write) 연산이 연결됩니다.

\(A(X)\)는 feature 차원 \(d\)에 공간적으로 작용하는 Delta Operator입니다:

\[ A(X) = I - \beta(X)\frac{k(X)k(X)^\top}{k(X)^\top k(X) + \epsilon} \]

이 구조는 반사 방향 \(k(X) \in \mathbb{R}^d\), value 벡터 \(v(X) \in \mathbb{R}^{d_v}\), 반사 강도 \(\beta(X) \in \mathbb{R}\)을 별도의 경량 신경망 branch로 학습합니다. 상수 \(\epsilon > 0\)은 수치 안정성을 보장합니다.

이론 분석에서는 \(k\)가 엄격하게 정규화되어 \(k^\top k = 1\)이라고 가정합니다. 이 조건 하에서 (\(\epsilon \to 0\)) 연산자는 다음과 같이 단순화됩니다:

\[ A(X) = I - \beta(X)k(X)k(X)^\top \]

\(X\)가 행렬이므로 연산자 \(A(X)\)는 value 차원 \(d_v\)에 대해 broadcast되며, hidden state의 모든 열에 기하학적 변환을 동시에 적용합니다.

같은 단위 노름 가정 하에서, \(A(X) = I - \beta(X)k(X)k(X)^\top\)를 식에 대입하면 동등한 덧셈형 rank-1 Delta 형태를 얻습니다:

\[ X_{l+1} = X_l + \beta(X_l)k(X_l)(v(X_l)^\top - k(X_l)^\top X_l) \]

이 형태는 같은 스칼라 \(\beta\)가 삭제 항 \(k^\top X\)와 쓰기 항 \(v^\top\)를 모두 조절한다는 점을 명시적으로 보여줍니다.

게이팅 함수 \(\beta(X)\)는 \([0, 2]\) 범위에 있도록 파라미터화됩니다:

\[ \beta(X) = 2 \cdot \sigma(\text{Linear}(G(X))) \]

여기서 \(G(\cdot)\)는 pooling, convolution, 또는 flattening 연산입니다. 이 특정 범위는 다음 섹션에서 분석할 풍부한 기하학적 해석을 제공하기 위해 선택되었습니다.

3. 분석: Delta Operator의 스펙트럼

Delta-Res block의 표현력은 연산자 \(A(X)\)의 스펙트럼 성질에서 나옵니다. 이 성질들은 학습된 게이트 \(\beta(X)\)로 제어됩니다.

3.1 스펙트럼 분해

정리 3.1 (Delta Operator의 스펙트럼): \(A = I - \beta kk^\top\)라 하자. 여기서 \(k \in \mathbb{R}^d\)는 단위 벡터 (\(k^\top k = 1\))이고 \(\beta \in \mathbb{R}\)는 스칼라다. \(A\)의 스펙트럼 \(\sigma(A)\)는:

\[ \sigma(A) = {\underbrace{1, 1, ..., 1}_{d-1 \text{ times}}, 1-\beta} \]

고유값 \(\lambda = 1 - \beta\)에 대응하는 고유벡터는 \(k\)입니다. 고유값 \(\lambda = 1\)에 대한 고유공간은 \(k\)의 직교 여공간 \(k^\perp = {u \in \mathbb{R}^d | k^\top u = 0}\)입니다.

증명 스케치:

\(k\)에 직교하는 벡터 \(u\) (\(k^\top u = 0\))에 대해: \(Au = (I - \beta kk^\top)u = u - \beta k(0) = u\). 따라서 \((d-1)\)차원 부공간 \(k^\perp\)의 모든 벡터가 고유값 1을 가집니다.
벡터 \(k\) 자체에 대해: \(Ak = (I - \beta kk^\top)k = k - \beta k(1) = (1-\beta)k\). 따라서 \(k\)는 고유값 \(1-\beta\)를 가집니다.

이 정리는 게이트 \(\beta(X)\)에 대한 명확하고 강력한 해석을 제공합니다. 단 하나의 스칼라를 학습함으로써, 네트워크는 상태 행렬의 모든 \(d_v\)개 열에 동시에 residual 변환의 기하학을 동적으로 제어할 수 있습니다.

행렬 상태로의 확장: 위 스펙트럼 명제들은 공간적(spatial)입니다. 즉 \(\mathbb{R}^d\)에서 선형 사상 \(u \mapsto Au\)를 설명합니다. hidden state가 행렬 \(X \in \mathbb{R}^{d \times d_v}\)이고 shortcut이 좌측 곱셈으로 작용하므로, \(d_v\)개 열 각각이 같은 \(A\)에 의해 독립적으로 변환됩니다. 벡터화 관점에서 유도된 선형 연산자는 \(I_{d_v} \otimes A\)입니다. 따라서 확장된 사상의 스펙트럼은 \(A\)의 고유값이 \(d_v\)번 반복된 것이고, 행렬식은 \(\det(A)^{d_v}\)입니다.

직교성 조건: \(A\)가 대칭이므로 특이값은 고유값의 절댓값과 일치합니다. 특히 \(A\)는 \(|1-\beta| = 1\)일 때, 즉 \(\beta \in {0, 2}\)일 때만 직교입니다. \(\beta \in (0, 2)\)에 대해 \(A\)는 \(k\)를 따라 이방성 수축(anisotropic contraction)을 수행합니다 (\(\beta > 1\)일 때 부호 반전).

따름정리 3.2 (공간 행렬식): 공간 특성 \(\mathbb{R}^d\)에 작용하는 Delta Operator \(A(X)\)의 행렬식은:

\[ \det(A(X)) = \prod_{i=1}^d \lambda_i = 1^{d-1} \cdot (1-\beta(X)) = 1 - \beta(X) \]

shortcut이 \(d_v\) value 열에 broadcast되므로 전체 행렬 상태 공간 \(\mathbb{R}^{d \times d_v}\)에서 유도된 행렬식은 \(\det(A(X))^{d_v} = (1-\beta(X))^{d_v}\)입니다. 따라서 \(\beta(X)\)는 공간 방향 \(k(X)\)를 따라 부호 있는 부피 변화를 제어합니다. 특히 \(\beta(X) > 1\)은 \(k\)를 따라 음의 공간 고유값(반사)을 도입하며, \(d_v\)가 홀수일 때만 확장된 상태 공간의 전체 방향이 뒤집힙니다.

3.2 기하학적 연산의 통합

정리 3.1은 \(\beta(X)\)의 범위 \([0, 2]\)가 연산자가 세 가지 기본 선형 변환 사이를 보간할 수 있게 함을 보여줍니다.

Identity Mapping (\(\beta(X) \to 0\)): \(\beta \to 0\)일 때 고유값 \(1-\beta \to 1\)입니다. \(A(X)\)의 모든 고유값이 1이 되므로 \(A(X) \to I\)입니다. \(\beta\)가 주입 항 \(\beta kv^\top\)도 조절하므로 전체 업데이트가 사라지며, \(X_{l+1} \approx X_l\)이 됩니다. 이 identity 동작은 매우 깊은 네트워크에서 신호 전파를 보존하는 데 중요합니다.

Orthogonal Projection (\(\beta(X) \to 1\)): \(\beta \to 1\)일 때 고유값 \(1-\beta \to 0\)입니다. 연산자 \(A(X)\)는 \(I - kk^\top\)가 되는데, 이는 초평면 \(k^\perp\)로의 직교 사영(rank \(d-1\))입니다. 입력 상태 \(X\)의 각 열에서 \(k\)에 평행한 성분이 residual을 더하기 전에 명시적으로 제거됩니다 ("망각"). 연산자가 특이(singular)가 되며 \(\det(A) \to 0\)입니다. 전체 block (식 2.5) 관점에서 이 체제는 replace-along-k로 해석할 수 있습니다: shortcut이 \(k\)-성분을 제거하고, rank-1 쓰기가 \(v^\top\)로 지정된 새로운 \(k\) 성분을 주입합니다.

Full Reflection (\(\beta(X) \to 2\)): \(\beta \to 2\)일 때 고유값 \(1-\beta \to -1\)입니다. 연산자 \(A(X)\)는 \(I - 2kk^\top\)가 되는데, 이는 표준 Householder 행렬입니다. 이는 \(X\)의 각 열을 \(k^\perp\)에 대해 완벽하게 반사시킵니다. 이것이 이 범위에서 변환이 직교이고 공간적으로 부피를 보존하는 유일한 경우이며, \(\det(A) \to -1\)입니다. 음의 공간 행렬식은 기저의 방향 변화(반사)를 의미합니다. identity 경우(\(\beta = 0\))와 함께 이는 \([0, 2]\)에서 shortcut 연산자 \(A\)가 직교인 유일한 설정입니다. 전체 block은 추가로 동기화된 rank-1 쓰기 항을 적용하여, 들어오는 상태의 반사와 \(k\)에 정렬된 쓰기를 수행합니다.

3.3 특수 경우: Gated Residual Learning

DDL의 중요한 성질은 게이팅 스칼라의 극한에서의 동작입니다. 게이트가 사라질 때 (\(\beta(X) \to 0\)), Delta Operator는 identity 행렬로 수렴하고 (\(A(X) \to I\)), 생성 항이 사라집니다. 결과적으로 업데이트 규칙은 다음과 같이 단순화됩니다:

\[ X_{l+1} = X_l \]

이는 identity mapping을 복원하며, 층을 완전히 건너뛸 수 있게 합니다. 이 동작은 매우 깊은 네트워크 훈련에 종종 필요한 zero-initialization 전략과 일치합니다.

반대로 \(\beta \approx 1\)일 때 층은 Gated Rank-1 Matrix ResNet으로 기능하며, \(\beta\)는 업데이트 크기를 제어하는 학습된 step size로 작용합니다. 이는 DDL이 값 주입과 동기적으로 결합된 곱셈적 기하학적 조절을 도입하여 residual learning을 일반화함을 보여줍니다.

3.4 대각 Feature 행렬 케이스

Delta Operator의 혼합(mixing) 성질을 더 잘 이해하기 위해, 입력 상태 \(X \in \mathbb{R}^{d \times d}\)가 정방 대각 행렬 \(X = \text{diag}(\lambda_1, ..., \lambda_d)\)인 특수한 경우를 고려해봅시다. 이는 feature가 value 차원에서 완벽하게 분리된 상태를 나타냅니다. \(A\)를 적용하면:

\[ (AX)_{ij} = (X - \beta kk^\top X)_{ij} = \lambda_i\delta_{ij} - \beta\lambda_j k_i k_j \]

구체적으로, 비대각 원소 (\(i \neq j\))는 \(-\beta\lambda_j k_i k_j\)가 되고, 대각 원소 (\(i = j\))는 \(\lambda_i(1 - \beta k_i^2)\)로 스케일됩니다. 이는 출력 feature \(i\)가 이제 입력 feature \(j\)의 크기에 의존하며, 기하학적 일관성 \(k_i k_j\)로 스케일됨을 의미합니다.

이 결과는 Delta block의 중요한 기능을 명확히 합니다: 제어된 feature 결합(coupling)을 유도한다는 것입니다. 들어오는 feature가 독립적이더라도, 영이 아닌 \(\beta\)는 반사 벡터 \(k\)의 투영에 비례하여 \(i\)번째와 \(j\)번째 모드 사이의 상호작용을 강제합니다.

\(\beta \to 1\) (투영)이면 shortcut이 각 열에서 \(k\)를 따라 성분을 제거하여, 쓰기 항이 \(v^\top\)로 지정된 새 \(k\)-성분을 재설정하기 전에 상태를 \(k^\perp\)로 매핑합니다. \(\beta \to 0\)이면 대각 구조가 보존됩니다.

3.5 벡터 Hidden State 동역학

DDL이 행렬 값 상태 \(X \in \mathbb{R}^{d \times d_v}\)에서 작동하지만, 자연스럽게 표준 벡터 기반 심층 학습을 특정 극한으로 포함합니다. 두 가지 구별되는 체제를 식별합니다:

스칼라 Value 극한 (\(d_v = 1\)): value 차원이 1로 축소되면, hidden state는 표준 feature 벡터 \(x \in \mathbb{R}^d\)로 퇴화합니다. 이 극한에서 value 업데이트 \(v\)는 스칼라 \(v \in \mathbb{R}\)가 됩니다. Delta 업데이트 규칙은 다음과 같이 단순화됩니다:

\[ x_{l+1} = x_l + \beta_l \underbrace{(v_l - k_l^\top x_l)}_{\gamma_l} k_l \]

여기서 기하학적 변환이 동적 스칼라 게이팅 메커니즘으로 축약됩니다. 항 \(\gamma_l\)은 업데이트 크기를 제안된 쓰기 값 \(v_l\)과 현재 투영 \(k_l^\top x_l\) 사이의 불일치에 결합하는 데이터 의존적 계수로 작용합니다.

독립 Feature 극한: 또는 섹션 3.4의 대각 경우를 행렬 대각선에 내장된 벡터 상태의 표현으로 볼 수 있습니다. 대각 분석에서 보듯이, Delta Operator는 \(\beta k_i k_j\) 항을 통해 feature 결합을 도입합니다. 표준 원소별 벡터 업데이트의 동작을 복원하려면 (feature가 공간적으로 혼합되지 않는 경우), 반사 벡터 \(k\)가 정규 기저와 정렬되어야 합니다 (즉, one-hot). 이 체제에서 Delta Operator는 원소별 게이팅 함수로 작용하며, feature 차원의 독립성을 엄격하게 보존합니다.

4. 최적화 및 Delta 구조와의 연결

"Deep Delta Learning"이라는 용어는 최근 효율적인 시퀀스 모델링에서 인기를 얻은 기본 업데이트 메커니즘인 Delta Rule과의 구조적 상동성을 반영합니다 (예: DeltaNet, Schlag et al., 2021; Yang et al., 2024).

4.1 Residual Learning을 위한 Delta Rule

표준 residual connection \(X_{l+1} = X_l + F(X_l)\)은 엄격한 덧셈 귀납 편향을 부과합니다. \(F\)가 생성한 정보는 단순히 축적됩니다. 이는 "residual accumulation"으로 이어질 수 있는데, 네트워크가 hidden state를 선택적으로 필터링할 명시적 메커니즘이 없기 때문에 노이즈나 간섭 feature가 층을 거쳐 지속됩니다.

DDL은 Delta Rule 구조를 depth 차원에 통합하여 이를 해결합니다. rank-1 residual 정의를 사용하여 Delta Residual 업데이트를 확장하면:

\[ X_{l+1} = X_l + \beta_l k_l \left(\underbrace{v_l^\top}_{\text{Write}} - \underbrace{k_l^\top X_l}_{\text{Erase}}\right) \]

이 공식화는 빠른 연관 메모리와 선형 attention에서 사용되는 Delta Rule 업데이트를 정확히 복원합니다. 항 \(k_l^\top X_l\)은 반사 벡터로의 상태의 현재 투영("오차" 또는 "오래된 메모리")을 나타냅니다. 항 \((v_l^\top - k_l^\top X_l)\)은 보정 신호로 작용합니다.

\(X_l \in \mathbb{R}^{d \times d_v}\)가 행렬이므로 항 \(k_l^\top X_l\)은 \(\mathbb{R}^{1 \times d_v}\)의 행 벡터를 생성하며, 모든 value 열의 \(k_l\)로의 투영을 나타냅니다. 업데이트는 삭제(파괴적)와 주입(생성적) 연산을 모두 프로젝터 \(k_l\)이 정의한 기하학적 방향을 따라 엄격하게 정렬하며, step size \(\beta_l\)로 조절됩니다.

\(\beta(X_l) \approx 1\)일 때, 이 뺄셈 항은 직교 투영으로 작용하여 들어오는 상태 \(X_l\)에서 \(k(X_l)\)에 평행한 성분을 효과적으로 지웁니다 (망각). \(\beta(X_l) \approx 2\)일 때, 이 항은 투영의 두 배를 빼서 부호 반전(반사)을 초래합니다. 이는 네트워크에 층별로 특정 feature 부공간을 선택적으로 정리하거나 재배향하는 유연한 메커니즘을 제공하여 간섭의 축적을 방지합니다.

4.2 DeltaNet 및 Householder 곱과의 관계

우리의 작업은 DeltaNet 구조(Schlag et al., 2021)와 이론적 연결고리를 공유합니다. DeltaNet은 Linear Transformer의 덧셈 축적을 메모리 업데이트를 위한 Delta Rule로 대체합니다. 우리는 **DDL이 DeltaNet 재귀의 depth-wise 동형(isomorphism)**임을 보여줍니다.

DeltaNet에서 hidden state (메모리) \(S_t\)는 시간 \(t\)에 걸쳐 진화합니다. 우리의 depth-wise 공식과 표기법을 통일하기 위해, 메모리 상태가 \(S_t \in \mathbb{R}^{d_k \times d_v}\)인 좌측 곱셈 의미론을 사용하여 DeltaNet 업데이트를 제시합니다:

\[ S_t = (I - \beta_t k_t k_t^\top)S_{t-1} + \beta_t k_t v_t^\top \]

여기서 연산자는 키 차원 \(d_k\)에 작용하며, 이는 DDL의 feature 차원 \(d\)와 유사합니다. 이를 depth \(l\)에 걸쳐 작용하는 우리의 Deep Delta Layer 업데이트와 비교하면:

\[ X_{l+1} = (I - \beta_l k_l k_l^\top)X_l + \beta_l k_l v_l^\top \]

여기서 \(v_l\)은 value branch의 벡터 출력입니다.

이는 직접적인 구조적 대응을 드러냅니다:

DeltaNet의 메모리 상태 \(S_t\) (차원 \(d_k \times d_v\))는 DDL의 feature activation \(X_l\) (차원 \(d \times d_v\))에 대응합니다.
두 구조 모두 rank-1 Householder 연산자를 사용하여 부공간 성분을 선택적으로 반사하거나 지웁니다. DeltaNet은 이를 시간 단계 \(t\)에 걸쳐 적용하는 반면, DDL은 네트워크 depth \(l\)에 걸쳐 적용합니다.
우리의 수정된 residual 업데이트 \(\beta_l k_l v_l^\top\)는 DeltaNet 쓰기 연산과 완벽하게 정렬됩니다. 생성 항에 \(\beta_l\)을 통합함으로써, 우리는 \(\beta_l\)을 depth-wise ODE의 층별 step size로 해석합니다. 이는 삭제 및 주입 성분이 동기적으로 조절되어, 업데이트가 상태 \(X\)의 일관된 기하학적 변환을 나타내도록 보장합니다.

따라서 DDL은 Delta Rule을 층별 feature 진화에 적용하는 것으로 해석될 수 있으며, 네트워크가 깊은 층으로 전파될 때 얕은 층의 feature를 망각하거나 재작성할 수 있게 합니다.

5. 관련 연구

이 작업은 심층 학습의 여러 핵심 연구 주제를 기반으로 합니다.

Gated 및 Invertible 구조: Highway Networks (Srivastava et al., 2015)는 residual 네트워크에 데이터 의존적 게이팅을 도입했지만, 그들의 게이트는 변환 자체를 수정하는 것이 아니라 identity 경로와 함수 경로 사이를 보간합니다. Invertible Residual Networks (i-ResNets) (Behrmann et al., 2019)는 \(F\)의 Lipschitz 상수를 제한하여 가역성을 보장하는데, 이는 normalizing flow 같은 응용에 유용합니다. DDL의 Delta shortcut 연산자는 \(1 - \beta \neq 0\)일 때 가역적이며 (\(\epsilon \to 0\) 분석에서), \(\beta = 2\)에서 직교 대합(orthogonal involution)이 됩니다 (Householder 반사). DDL은 전역적으로 가역성을 강제하지 않습니다. 대신 네트워크가 준-가역 전이가 유익한 때와 의도적으로 특이한 (투영적) 전이가 제어된 망각에 유용한 때를 학습할 수 있게 합니다.

직교 및 유니터리 네트워크: 상당한 연구가 기울기 안정성을 개선하고 기하학적 구조를 보존하기 위해 네트워크 가중치를 직교 또는 유니터리로 제한하는 데 집중해왔습니다 (Arjovsky et al., 2016; Jing et al., 2017). Householder 반사는 직교 행렬을 파라미터화하는 고전적 방법입니다. 이러한 방법은 직교성을 엄격한 제약으로 강제합니다. 대조적으로, 우리의 Delta Residual Network는 게이트 \(\beta(x)\)를 통해 identity와 직교성에서 벗어나는 것을 학습하며, 순수 투영이나 반사로 완화할 수 있는 소프트한 적응적 제약을 제공합니다.

Neural ODE: Neural ODE (Chen et al., 2018)는 feature의 연속적 진화를 모델링합니다. 표준 ResNet은 단순 ODE \(\dot{X} = F(X)\)의 이산화입니다. 우리가 제안한 구조는 기저 동역학을 \(\dot{X} = \beta(X)k(X)(v(X)^\top - k(X)^\top X)\)로 변경하여, 행렬 상태에 적용되는 상태 의존적 투영 항을 도입합니다. 이는 여러 value 차원에 걸쳐 수축적이거나 진동적인 동작을 나타낼 수 있는 훨씬 더 풍부한 학습 가능한 동역학계 패밀리를 허용합니다.

6. 결론: 표현력의 확장과 남은 과제

DDL은 적응적 기하학적 residual connection 위에 구축된 새로운 구조를 제시합니다. 분석을 통해 그 핵심 구성 요소인 Delta Operator가 identity mapping, projection, 그리고 reflection을 하나의 연속적으로 미분 가능한 모듈로 통합함을 입증했습니다. 이 통합은 단순한 학습된 스칼라 게이트로 제어되며, 층간 전이 연산자의 스펙트럼을 동적으로 형성합니다.

네트워크가 데이터 의존적 방식으로 음의 고유값을 가진 변환을 학습할 수 있게 함으로써, DDL은 residual learning 패러다임의 기본 이점을 유지하면서 표현력에서 원리적이고 상당한 증가를 제공합니다.

하지만 논문이 제시하지 않은 부분도 명확합니다. 실제 대규모 벤치마크에서의 경험적 검증이 부재합니다. ImageNet, COCO 같은 표준 vision 과제나 GLUE, SQuAD 같은 NLP 벤치마크에서 DDL이 실제로 표준 ResNet이나 Transformer보다 우수한 성능을 보이는지는 아직 증명되지 않았습니다. 이론적 우아함이 실전 성능 개선으로 이어진다는 보장은 없죠.

또한 추가적인 파라미터 오버헤드와 계산 복잡도에 대한 분석이 필요합니다. \(k(X)\), \(\beta(X)\), \(v(X)\)를 각각 추정하는 branch들이 전체 모델 크기와 추론 속도에 미치는 영향은? rank-1 업데이트가 간단해 보이지만, 각 층에서 추가적인 순전파 연산이 필요하므로 실제 wall-clock time이 증가할 수 있습니다.

가장 흥미로운 질문은 "언제 DDL이 필요한가?"입니다. 저자들은 진동이나 대립적 행동 같은 복잡한 동역학을 모델링할 때 음의 고유값이 필요하다고 주장합니다. 하지만 실제 vision이나 언어 과제에서 이런 동역학이 얼마나 자주 나타날까요? 대부분의 실용적 문제에서는 표준 ResNet의 단조적 feature 변환으로도 충분할 수 있습니다. DDL의 진가는 특정 도메인(예: 물리 시뮬레이션, 시계열 예측, 강화학습)에서 더 명확히 드러날 가능성이 높습니다.

결국 Deep Delta Learning은 residual connection의 이론적 한계를 정확히 식별하고, 수학적으로 우아한 해결책을 제시했다는 점에서 의미 있는 기여입니다. Householder 변환이라는 고전적 도구를 심층 학습에 접목시킨 것은 창의적이며, Delta Rule과의 연결은 DeltaNet 같은 최근 시퀀스 모델링 연구와의 이론적 통일을 보여줍니다. 하지만 실전 배포를 위해서는 대규모 실험적 검증, 효율성 분석, 그리고 언제 이 추가적인 복잡성이 정당화되는지에 대한 명확한 가이드라인이 필요합니다.