Black-Box On-Policy Distillation of Large Language Models

🏷️ 논문 LLM

대규모 언어 모델의 지식 증류는 거대한 교사 모델의 능력을 작고 효율적인 학생 모델로 압축하는 핵심 기술입니다. 하지만 GPT-5나 Gemini 같은 최신 모델들은 API로만 접근 가능하고, 내부 확률 분포나 히든 스테이트를 공개하지 않습니다. 이런 블랙박스 환경에서는 전통적인 화이트박스 증류 기법들이 무용지물이 되죠.

Microsoft Research는 이 문제를 생성적 적대 신경망(GAN)의 프레임워크로 재해석했습니다. 학생 모델을 생성자로, 별도의 판별자를 두어 교사과 학생의 응답을 구분하도록 했습니다. 판별자가 구분하지 못할 정도로 교사을 따라하도록 학생을 훈련시키는 과정에서, 학생은 자신이 생성한 응답(온폴리시)으로부터 학습하게 됩니다.

저자들은 LMSYS-Chat 데이터셋으로 Qwen2.5와 Llama3 계열 모델들을 증류했고, 14B 파라미터 모델이 교사인 GPT-5-Chat에 필적하는 성능을 달성했다고 보고합니다. 특히 분포 외 데이터에서의 일반화 성능이 두드러졌는데, 이는 지도학습 기반의 기존 방법과 차별화되는 강점입니다.

T. Ye, L. Dong, Z. Chi, X. Wu, S. Huang and F. Wei, "Black-Box On-Policy Distillation of Large Language Models", arXiv preprint arXiv:2511.10643, 2025.

1-Black-BoX.png

요약

아키텍처

사용 모델

데이터셋

평가 매트릭

훈련 방법

논문 상세

서론

화이트박스 지식 증류는 KL divergence를 통해 교사과 학생의 출력 분포를 정렬하거나, 히든 스테이트를 매칭하는 방식으로 작동합니다. 하지만 GPT-5 같은 API 모델은 텍스트 출력만 제공하므로, 확률 레벨의 지도 신호가 없습니다. 게다가 토크나이저가 다르면 로짓 기반 목적함수 자체가 적용 불가능하죠.

기존 블랙박스 증류의 표준인 SeqKD(Sequence-level Knowledge Distillation)는 단순히 교사의 응답으로 지도학습을 수행합니다. 이는 교사이 생성한 데이터에만 의존하는 오프폴리시(off-policy) 방식입니다. 최근 화이트박스 연구들은 학생이 자체 생성한 응답으로 학습하는 온폴리시(on-policy) 방식이 mode-seeking 행동을 유도하고 노출 편향(exposure bias)을 줄인다고 밝혔습니다. 하지만 블랙박스에서는 학생이 만든 응답에 대한 교사의 피드백이 없어 온폴리시 학습이 불가능했습니다.

GAD는 이 간극을 메웁니다. 판별자가 암묵적 피드백을 제공하여, 확률 공간 접근 없이도 학생이 자신의 생성물로부터 학습할 수 있게 만듭니다. 강화학습 관점에서 보면, 판별자는 학생 정책과 함께 진화하는 온폴리시 보상 모델입니다. RLHF의 고정된 보상 모델과 달리, 계속 적응하며 보상 해킹(reward hacking)을 방지합니다.

GAD

프롬프트 \(x\)가 데이터셋 \(\mathcal{D}\)에서 샘플링되면, 교사 분포 \(p(y|x)\)는 응답 \(y_t\)를 생성합니다. 학생 분포 \(q_\theta(y|x)\)는 파라미터 \(\theta\)로 매개변수화됩니다. 블랙박스 설정에서는 \(p(y|x)\)에 접근할 수 없고, 교사이 생성한 텍스트만 관찰 가능합니다.

훈련 데이터셋은 \(\mathcal{T} = {(x, y_t)}\)로 구성됩니다. 생성자 \(G\)는 학생 모델이며, 판별자 \(D\)는 프롬프트와 응답 쌍 \([x, y]\)를 입력받아 스칼라 점수 \(D([x, y])\)를 출력합니다. 미니맥스 게임의 가치 함수는:

\[ \min_G \max_D V(G, D) = \mathbb{E}_{(x, y_t) \sim \mathcal{T}} \left[ -\log \sigma(D(y_t) - D(G(x))) \right] \]

여기서 \(\sigma(\cdot)\)는 시그모이드 함수입니다. Bradley-Terry 모델을 사용해 교사과 학생 응답 간 쌍대 선호도를 포착합니다.

생성자의 목적함수는:

\[ \max_G \mathbb{E}_{(x, y_t) \sim \mathcal{T}} [D(G(x))] \]

샘플링 연산이 미분 불가능하므로, \(D(G(x))\)를 보상으로 취급하고 정책 그래디언트로 최적화합니다. 저자들은 GRPO(Group Relative Policy Optimization) 알고리즘을 사용했습니다.

판별자의 손실함수는:

\[ \min_D \mathbb{E}_{(x, y_t) \sim \mathcal{T}} \left[ -\log \sigma(D(y_t) - D(G(x))) \right] \]

Bradley-Terry 손실로 교사 응답에 더 높은 점수를 부여하도록 학습합니다.

구현

각 프롬프트 \(x\)에 대해 \(N=8\)개의 학생 응답 \({y_i^s}_{i=1}^N\)을 샘플링하고, 판별자로부터 보상 \({r_i^s}_{i=1}^N\)을 받습니다. \(i\)번째 응답의 어드밴티지는:

\[ A_i = \frac{r_i^s - \text{mean}({r_j^s}_{j=1}^N)}{\text{std}({r_j^s}_{j=1}^N)} \]

생성자는 다음 목적함수로 훈련됩니다:

\[ \max_G \mathbb{E}_{(x, y_t) \sim \mathcal{T}, {y_i^s}_{i=1}^N \sim q_G(\cdot|x)} \left[ \frac{1}{N} \sum_{i=1}^N A_i \right] \]

판별자는 각 학생 응답 \(y_i^s\)와 교사 응답 \(y_t\)를 쌍으로 만들어, 그룹 내 Bradley-Terry 손실로 학습합니다:

\[ \min_D \mathbb{E}_{(x, y_t) \sim \mathcal{T}, {y_i^s}_{i=1}^N \sim q_G(\cdot|x)} \left[ \frac{1}{N} \sum_{i=1}^N -\log \sigma(D(y_t) - D(y_i^s)) \right] \]

Warmup 전략

GAD 훈련 전 1 에폭의 공동 워밍업이 성능에 결정적입니다. 생성자는 교사 응답에 대한 cross-entropy 손실로, 판별자는 동일 데이터에서 Bradley-Terry 손실로 워밍업합니다. 이는 생성자와 판별자의 균형을 맞춰 효과적인 적대적 최적화를 가능케 합니다.

Ablation 연구 결과:

생성자 워밍업 없이는 초기 단계에서 교사-학생 분포 격차가 커서 판별자가 너무 쉽게 구분해버립니다. 판별자 워밍업 없이는 생성자와의 불균형으로 유의미한 피드백을 제공하지 못합니다.

실험 결과

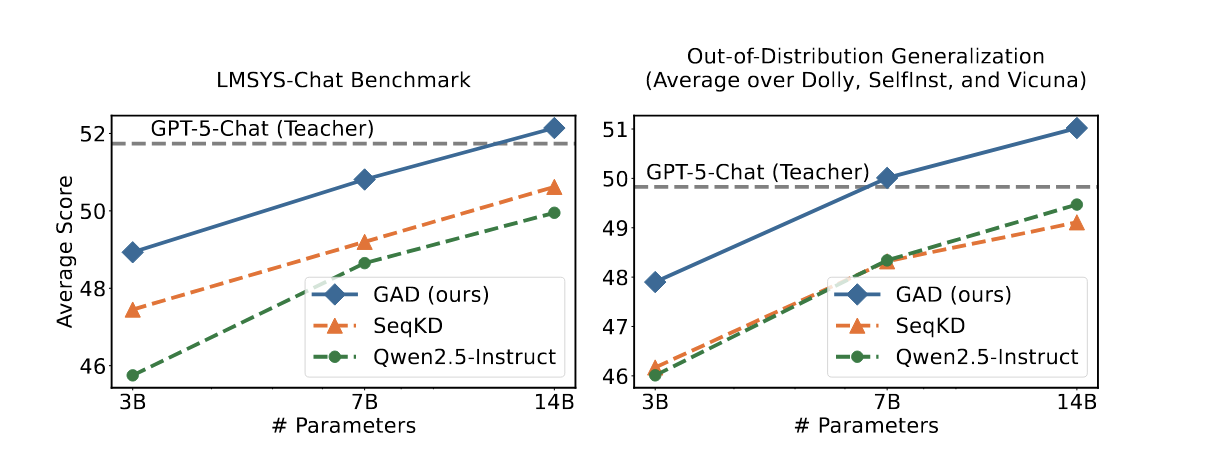
LMSYS-Chat 테스트셋에서 Qwen2.5-3B GAD는 Qwen2.5-7B SeqKD와 동등한 성능(GPT-4o 점수 48.9 vs 49.2)을 보였습니다. Qwen2.5-14B GAD는 52.1점으로 교사 GPT-5-Chat(51.7)에 근접했습니다.

분포 외 일반화에서 GAD의 강점이 두드러집니다. Dolly, SelfInst, Vicuna 평균에서:

저자들은 이를 지도학습 대비 강화학습의 우수한 일반화 능력으로 설명합니다.

인간 평가에서도 GAD는 증류 전 모델 대비 56-68% 승률, SeqKD 대비 44-68% 승률을 기록했습니다.

SeqKD는 지엽적 패턴에 과적합

N-gram 중첩도 분석 결과, SeqKD 학생은 교사보다 높은 F1 점수를 보이지만 GPT-4o 평가는 더 낮습니다. 이는 지도학습이 지엽적 어휘 패턴을 암기하는 경향이 있음을 시사합니다. 반면 GAD는 교사의 전역적 스타일 특성을 더 잘 포착합니다.

Toy 실험에서 이 현상이 명확히 드러납니다. 가우시안 혼합 분포를 교사으로 설정하고, 단일 가우시안 학생을 훈련시켰을 때:

이러한 mode-seeking이 LLM 증류에서 더 효과적입니다.

보상 해킹 방지

오프폴리시 설정에서는 학생을 1 에폭 SeqKD로 먼저 훈련하고, 고정된 학생 출력으로 판별자를 2 에폭 훈련한 뒤, 이를 고정 보상 모델로 사용합니다. 결과는 참담했습니다. 300 스텝 이후 응답 길이가 1300 토큰까지 폭증하며 보상 해킹이 발생했습니다.

GAD의 온폴리시 판별자는 수천 스텝 동안 안정적으로 작동하며 보상 해킹 징후가 없었습니다. 판별자가 학생과 함께 진화하며 지속적으로 적절한 피드백을 제공하기 때문입니다.

강화학습 프레임워크 내 구현

GAD는 기존 RL 프레임워크(verl 등)로 구현 가능합니다:

RL 용어

GAD 대응

차이점

Policy Model

Generator (학생 LLM)

-

Reward Model

Discriminator

RLHF는 고정, GAD는 온폴리시로 공진화

Reward

\(D(G(x))\)

-

RLHF의 고정 보상 모델이 보상 해킹에 취약한 반면, GAD의 판별자는 미니맥스 게임에서 지속적으로 업데이트됩니다.

토크나이저 불일치 상황에서의 적용

Qwen2.5-14B를 교사으로, Llama 계열을 학생으로 증류한 실험에서도 GAD가 효과적이었습니다. 토크나이저가 달라 화이트박스 KLD 정렬이 불가능한 상황임에도, GAD는 SeqKD를 대부분 설정에서 능가했습니다 (Llama-3.1-8B LMSYS: 49.0 vs 49.6, Vicuna: 49.4 vs 49.7).

결론

GAD는 블랙박스 LLM 증류의 핵심 난제를 우아하게 해결합니다. 확률 레벨 지도 없이도, 적대적 프레임워크를 통해 학생이 자신의 응답으로부터 학습하는 온폴리시 메커니즘을 구현했습니다. 판별자가 암묵적이고 적응적인 보상 신호를 제공하며, 학생 정책과 공진화하여 보상 해킹을 방지합니다.

다만 몇 가지 한계도 명확합니다. 첫째, 판별자 훈련으로 인한 추가 계산 비용이 발생합니다(Qwen2.5-14B 증류 시 H100 16개로 30시간). 둘째, 워밍업 전략의 하이퍼파라미터(에폭 수, 학습률)가 성능에 민감하며, 이는 추가 튜닝 부담입니다. 셋째, GPT-4o 자동 평가에 의존하는 것은 편향 가능성이 있습니다.

그럼에도 GAD가 제시한 방향은 주목할 가치가 있습니다. API 모델의 지식을 효과적으로 전달받을 수 있다는 것은, 폐쇄형 프론티어 모델의 능력을 오픈소스 생태계로 민주화할 가능성을 열어줍니다. Mode-seeking 행동이 실제 LLM 증류에서도 유효하다는 실증적 증거 또한 향후 연구의 토대가 될 것입니다.

개인적으로는 판별자의 아키텍처를 최적화하거나, 다중 판별자 앙상블을 시도하는 후속 연구가 흥미로울 것 같습니다. 또한 교사-학생 간 용량 차이가 극단적일 때(예: GPT-5 → 1B 모델) GAD의 효과가 유지되는지도 궁금한 지점입니다.